(本小题满分12分)已知数列 为等差数列,其中
为等差数列,其中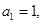
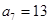 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列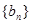 满足
满足 ,
,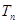 为数列
为数列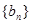 的前
的前 项和,当不等式
项和,当不等式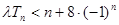 (
(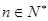 )恒成立时,求实数
)恒成立时,求实数 的取值范围.
的取值范围.
设函数 (Ⅰ) 当
(Ⅰ) 当 时,求函数
时,求函数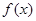 的极值;
的极值;
(Ⅱ)当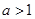 时,讨论函数
时,讨论函数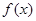 的单调性.(Ⅲ)(理科)若对任意
的单调性.(Ⅲ)(理科)若对任意 及任意
及任意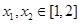 ,恒有
,恒有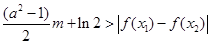 成立,求实数
成立,求实数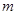 的取值范围.
的取值范围.
已知椭圆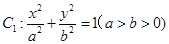 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线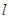 恰好与圆
恰好与圆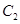 相切.
相切.
(Ⅰ)已知椭圆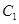 的离心率;
的离心率;
(Ⅱ)若 的最大值为49,求椭圆C
的最大值为49,求椭圆C 的方程.
的方程.
如图,在三棱锥 中,侧面
中,侧面 与侧面
与侧面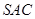 均为等边三角形,
均为等边三角形, ,
,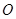 为
为 中点.
中点.
(Ⅰ)证明: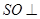 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
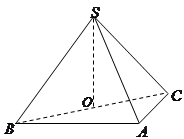
盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:(1)取到的2只都是次品;(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品.
已知在 中,
中, 所对的边分别为
所对的边分别为 ,若
,若 且
且 .
.
(Ⅰ)求角A、B、C的大小;
(Ⅱ)设函数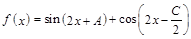 ,求函数
,求函数 的单调递增区间,并指出它相邻两对称轴间的距离.
的单调递增区间,并指出它相邻两对称轴间的距离.