某工厂生产某种产品,每日的成本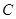 (单位:万元)与日产量x(单位:吨)满足函数关系式
(单位:万元)与日产量x(单位:吨)满足函数关系式 ,每日的销售额S(单位:万元)与日产量x的函数关系式
,每日的销售额S(单位:万元)与日产量x的函数关系式
已知每日的利润 ,且当
,且当 时,
时,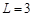 .(1)求
.(1)求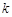 的值;(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值。
的值;(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值。
某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1 000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为x (0<x<1),则出厂价相应提高的比例为0.75x, 同时预计年销售量增加的比例为0.6x.已知年利润=(出厂价-投入成本)×年销售量.
(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度利润比上年有所增加,问投入成本增加的比例x应在什么范围内?
给出下列两个条件:(1)f( +1)=x+2
+1)=x+2 ;
;
(2)f(x)为二次函数且f(0)=3,f(x+2)-f(x)=4x+2.试分别求出f(x)的解析式.

1.(北京市西城外语学校·2010届高三测试)设函数f(x)的定义域为R,当x<0时f(x)>1,且对任意的实数x,y∈R,有
(Ⅰ)求f(0),判断并证明函数f(x)的单调性;
(Ⅱ)数列 满足
满足 ,且
,且 ,数列
,数列 满足
满足
①求数列 通项公式。
通项公式。
②求数列 的前n项和Tn的最小值及相应的n的值.
的前n项和Tn的最小值及相应的n的值.
(北京市西城外语学校·2010届高三测试)已知等差数列{an}中,a2=6,a5=15.若bn=a2n ,求数列{bn}的前5项和。
(河南省许昌平顶山·2010届高三调研){an}是等差数列,a1>0,a2009+a2010>0,a2009·a2010<0,使前n项和Sn>0成立的最大自然数n。