本题10分)
操作：小明准备制作棱长为1cm的正方体纸盒，现选用一些废弃的圆形纸片进行如下设计：
纸片利用率=×100%
发现：（1）方案一中的点A、B恰好为该圆一直径的两个端点．你认为小明的这个发现是否正确，请说明理由．
（2）小明通过计算，发现方案一中纸片的利用率仅约为38.2%．请帮忙计算方案二的利用率，并写出求解过程．
探究：（3）小明感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率．
小明有一张地图，上面有A、B、C三地，但被墨迹污染，C地具体位置看不清楚了，但知道C地在A地的北偏东30°，在B地的南偏东45°，请你在图中画一画，试着帮他确定C地在地图上的位置。
知识是用来为人类服务的，我们应该把它们用于有意义的方．下面就两个情景请你作出评判．
情景一：从教室到图书馆，总有少数同学不走人行道而横穿草坪，这是为什么呢？试用所学数学知识来说明这个问题。
情景二：A、B是河流l两旁的两个村庄，现要在河边修一个抽水站向两村供水，问抽水站修在什么地方才能使所需的管道最短？请在图中表示出抽水站点P的位置，并说明你的理由：。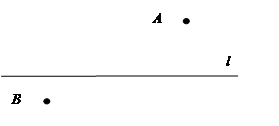
你赞同以上哪种做法？你认为应用数学知识为人类服务时应注意什么？
已知：线段AB=6厘米，点C是AB的中点，点D在AC的中点，求线段BD的长。
先化简，再求值：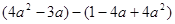 
其中a =－2。
有理数
，
，
在数轴上的对应点如图所示，且，，满足条件10
=5
=2
=10.
（1）求，，的值；
（2）求
的值。