知识是用来为人类服务的，我们应该把它们用于有意义的方．下面就-优题课

题文

知识是用来为人类服务的，我们应该把它们用于有意义的方．下面就两个情景请你作出评判．
情景一：从教室到图书馆，总有少数同学不走人行道而横穿草坪，这是为什么呢？试用所学数学知识来说明这个问题。

情景二：A、B是河流l两旁的两个村庄，现要在河边修一个抽水站向两村供水，问抽水站修在什么地方才能使所需的管道最短？请在图中表示出抽水站点P的位置，并说明你的理由：。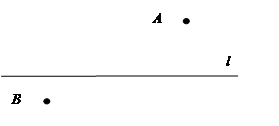

你赞同以上哪种做法？你认为应用数学知识为人类服务时应注意什么？

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

已知：如图，四边形 $ABCD$ 为平行四边形，点 $E$ 、 $A$ 、 $C$ 、 $F$ 在同一直线上， $AE = CF$ ．

求证：（1） $ΔADE ≅ ΔCBF$ ；

（2） $ED / / BF$ ．

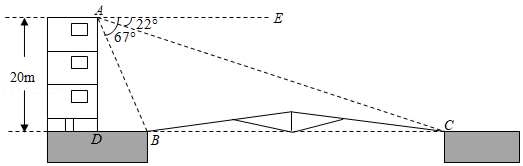
政府将要在某学校大楼前修一座大桥．如图，宋老师测得大楼的高是20米，大楼的底部 $D$ 处与将要修的大桥 $BC$ 位于同一水平线上，宋老师又上到楼顶 $A$ 处测得 $B$ 和 $C$ 的俯角 $∠ EAB$ ， $∠ EAC$ 分别为 $67 °$ 和 $22 °$ ，宋老师说现在我能算出将要修的大桥 $BC$ 的长了．同学们：你知道宋老师是怎么算的吗？请写出计算过程（结果精确到0.1米）．

其中 $\sin 67 ° \approx \frac{12}{13}$ ， $\cos 67 ° \approx \frac{5}{13}$ ， $\tan 67 ° \approx \frac{12}{5}$ ， $\sin 22 ° \approx \frac{3}{8}$ ， $\cos 22 ° \approx \frac{15}{16}$ ， $\tan 22 ° \approx \frac{2}{5}$

先化简，再求值： $\frac{1}{x} + \frac{2 x + 6}{x^{2} - 4 x + 4} \cdot \frac{x - 2}{x^{2} + 3 x}$ ，其中 $x = \sqrt{2} + 2$ ．

计算： ${(3 - π)}^{0} - \sqrt{12} + {(\frac{1}{3})}^{- 2} + 4 \sin 60 ° - (- 1)$ ．

在平面直角坐标系中，如果一个点的横坐标与纵坐标相等，则称该点为"雁点"．例如 $(1, 1)$ ， $(2021, 2021) \dots$ 都是"雁点"．

（1）求函数 $y = \frac{4}{x}$ 图象上的"雁点"坐标；

（2）若抛物线 $y = a x^{2} + 5 x + c$ 上有且只有一个"雁点" $E$ ，该抛物线与 $x$ 轴交于 $M$ 、 $N$ 两点（点 $M$ 在点 $N$ 的左侧）．当 $a > 1$ 时．

①求 $c$ 的取值范围；

②求 $∠ EMN$ 的度数；

（3）如图，抛物线 $y = - x^{2} + 2 x + 3$ 与 $x$ 轴交于 $A$ 、 $B$ 两点（点 $A$ 在点 $B$ 的左侧）， $P$ 是抛物线 $y = - x^{2} + 2 x + 3$ 上一点，连接 $BP$ ，以点 $P$ 为直角顶点，构造等腰 $Rt Δ BPC$ ，是否存在点 $P$ ，使点 $C$ 恰好为"雁点"？若存在，求出点 $P$ 的坐标；若不存在，请说明理由．

试卷网试题网古诗词网作文网范文网

Copyright ©2020-2025 优题课 youtike.com 版权所有

粤ICP备20024846号