(本小题满分10分)如图,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、B重合),过点E的反比例函数 的图象与边BC交于点F.
的图象与边BC交于点F.
(1)若△OAE、△OCF的而积分别为 .且
.且 ,求k的值.
,求k的值.
(2)若OA=2,0C=4,问当点E运动到什么位置时,四边形OAEF的面积最大,其最大值为多少?
(本题3分+3分)如图,△ABC中,∠B=90°,AB=6,BC=8,点P从点A开始沿边AB向点B以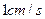 的速度移动,与此同时,点Q从点B开始沿边BC向点C以
的速度移动,与此同时,点Q从点B开始沿边BC向点C以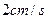 的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,
的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动,
问:(1)经过几秒,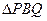 的面积等于
的面积等于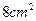 ?(2)
?(2) 的面积会等于△ABC的面积的一半吗?若会,请求出此时的运动时间;若不会,请说明理由.
的面积会等于△ABC的面积的一半吗?若会,请求出此时的运动时间;若不会,请说明理由.
(本题2分+2分+2分)已知二次函数y= -x2-2x+3
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y < 0时,x的取值范围;
(3)将此图象沿x轴向左平移几个单位,可使平移后所得图象经过坐标原点?请写出平移后图象与x轴的另一个交点的坐标.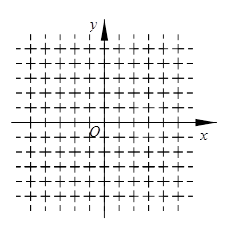
(本题2分+4分)已知函数 (
( 是常数).
是常数).
⑴求证:不论 为何值,该函数的图象都经过
为何值,该函数的图象都经过 轴上的一个定点;
轴上的一个定点;
⑵若该函数的图象与 轴只有一个交点,求
轴只有一个交点,求 的值.
的值.
(本题6分)已知,在△ABC中,∠C= ,斜边
,斜边 =5,两直角边
=5,两直角边 的长分别是关于
的长分别是关于 的方程
的方程 的两个根,求△ABC的周长.
的两个根,求△ABC的周长.
(本题3分+2分)先化简,再求值: ,其中
,其中 满足x2-2x-4=0
满足x2-2x-4=0