已知椭圆 的离心率为
的离心率为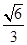 ,右焦点为(
,右焦点为(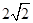 ,0),斜率为1的直线
,0),斜率为1的直线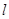 与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
与椭圆G交与A、B两点,以AB为底边作等腰三角形,顶点为P(-3,2).
(1)求椭圆G的方程;(2)求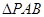 的面积.
的面积.
函数 .
.
(1)求函数f(x)的最小正周期;
(2)在△ABC中,a,b,c分别为内角A,B,C的对边,且 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.
定义在 上的函数
上的函数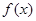 满足对任意
满足对任意 都有
都有 .
.
且 时,
时, ,
,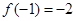
(1)求证: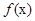 为奇函数;
为奇函数;
(2)试问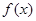 在
在 上是否有最值?若有,求出最值;若无,说明理由;
上是否有最值?若有,求出最值;若无,说明理由;
(3)若 对任意
对任意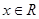 恒成立,求实数
恒成立,求实数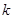 的取值范围.
的取值范围.
设 为实数,函数
为实数,函数 .
.
(1)若函数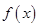 是偶函数,求实数
是偶函数,求实数 的值;
的值;
(2)若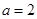 ,求函数
,求函数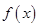 的最小值;
的最小值;
(3)对于函数 ,在定义域内给定区间
,在定义域内给定区间 ,如果存在
,如果存在 ,满足
,满足 ,则称函数
,则称函数 是区间
是区间 上的“平均值函数”,
上的“平均值函数”,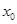 是它的一个“均值点”.如函数
是它的一个“均值点”.如函数 是
是 上的平均值函数,
上的平均值函数, 就是它的均值点.现有函数
就是它的均值点.现有函数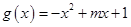 是区间
是区间 上的平均值函数,求实数
上的平均值函数,求实数 的取值范围.
的取值范围.
某村电费收取有以下两种方案供农户选择:
方案一:每户每月收管理费2元,月用电不超过30度时,每度0.5元,超过30度时,超过部分按每度0.6元收取.
方案二:不收管理费,每度0.58元.
(1)求方案一收费 元与用电量
元与用电量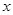 (度)间的函数关系;
(度)间的函数关系;
(2)老王家九月份按方案一交费35元,问老王家该月用电多少度?
(3)老王家月用电量在什么范围时,选择方案一比选择方案二更好?
已知函数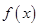 是二次函数,且满足
是二次函数,且满足 ;函数
;函数 .
.
(1)求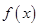 的解析式;
的解析式;
(2)若 ,且
,且 对
对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.