在公比为 的等比数列
的等比数列 中,
中,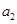 与
与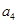 的等差中项是
的等差中项是 .
.
(Ⅰ)求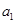 的值;
的值;
(Ⅱ)若函数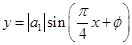 ,
,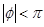 ,的一部分图像如图所示,
,的一部分图像如图所示,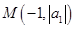 ,
, 为图像上的两点,设
为图像上的两点,设 ,其中
,其中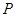 与坐标原点
与坐标原点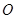 重合,
重合,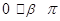 ,求
,求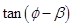 的值.
的值.
(本小题满分12分)
已知函数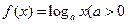 且
且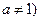 在区间[,4]上的最大值与最小值的差为3,求
在区间[,4]上的最大值与最小值的差为3,求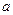 .
.
.(本题满分12分)
如图所示, ⊥矩形
⊥矩形 所在的平面,
所在的平面, 分别是
分别是 、
、 的中点,
的中点,
(1)求证: ∥平面
∥平面 ;
;
(2)求证: ⊥
⊥ ;
;
(3)若 ,求证:平面
,求证:平面 ⊥平面
⊥平面 .
.
(本小题满分12分)
已知函数 .
.
(1)判断其奇偶性;
(2)指出该函数在区间(0,1)上的单调性并证明;
(3)利用(1)、(2)的结论,指出该函数在(-1,0)上的增减性.
(本小题满分12分)
已知两直线 :
: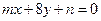 和
和 :
: ,
,
(1)若 与
与 交于点
交于点 ,求
,求 的值;
的值;
(2)若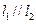 ,试确定
,试确定 需要满足的条件;
需要满足的条件;
(3)若l1⊥l2 ,试确定 需要满足的条件.
需要满足的条件.
(本小题满分10分)
如图所示的一个三视图中,右面是一个长方体截去一角所得多面体的直观图,它的正视 图和侧视图在下面画出(单位:cm)
图和侧视图在下面画出(单位:cm)

(1)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(2)按照给出的尺寸,求该多面体的体积;