如图,四棱柱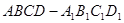 中,
中,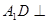 平面
平面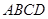 ,底面
,底面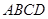 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱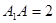 ,
,
(Ⅰ)证明: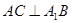 ;
;
(Ⅱ)若棱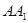 上存在一点
上存在一点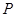 ,使得
,使得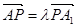 ,
,
当二面角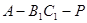 的大小为
的大小为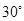 时,求实数
时,求实数 的值.
的值.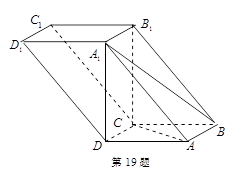
设关于x的方程sin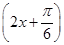 =
=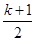 在
在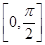 内有两个不同根α、β,求α+β的值及k的取值范围.
内有两个不同根α、β,求α+β的值及k的取值范围.
如图:某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b
(1)求这段时间的最大温差.
(2)写出这段曲线的函数解析式.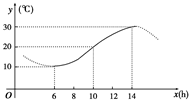
单摆从某点开始左右摆动,它离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=6sin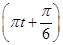 .求:
.求:
(1)单摆开始摆动(t=0)时离开平衡位置的位移;
(2)单摆离开平衡位置的最大位移;
(3)单摆来回摆动一次所需要的时间.
已知电流I与时间t的关系式为I=Asin(ωt+φ).
(1)如图是I=Asin(ωt+φ)(ω>0,|φ|<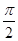 )在一个周期内的图象,根据图中数据求解析式.
)在一个周期内的图象,根据图中数据求解析式.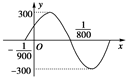
(2)如果t在任意一段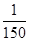 秒的时间内,电流I=Asin(ωT+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?
秒的时间内,电流I=Asin(ωT+φ)都能取得最大值和最小值,那么ω的最小正整数值是多少?
已知飞机从甲地按北偏东30°的方向飞行2000km到达乙地,再从乙地按南偏东30°的方向飞行2000km到达丙地,再从丙地按西南方向飞行1000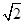 km到达丁地,问丁地在甲地的什么方向?丁地距甲地多远?
km到达丁地,问丁地在甲地的什么方向?丁地距甲地多远?