命题“若一个数是负数，则它的平方是正数”的逆命题是（ ）
| A．“若一个数是负数，则它的平方不是正数” |
| B．“若一个数的平方是正数，则它是负数” |
| C．“若一个数不是负数，则它的平方不是正数” |
| D．“若一个数的平方不是正数，则它不是负数” |
已知f（x）是定义域为正整数集的函数，对于定义域内任意的k，若f（k）≥k2成立，则f（k+1）≥（k+1）2成立，下列命题成立的是（）
| A．若f（3）≥9成立，则对于任意k≥1，均有f（k）≥k2成立； |
| B．若f（4）≥16成立，则对于任意的k≥4，均有f（k）＜k2成立； |
| C．若f（7）≥49成立，则对于任意的k＜7，均有f（k）＜k2成立； |
| D．若f（4）=25成立，则对于任意的k≥4，均有f（k）≥k2成立 |
某个命题与自然数n有关，若n=k（k∈N*）时命题成立，那么可推得当n=k+1时该命题也成立．现已知当n=5时，该命题不成立，那么可推得（）
| A．当n=6时，该命题不成立 | B．当n=6时，该命题成立 |
| C．当n=4时，该命题不成立 | D．当n=4时，该命题成立 |
用数学归纳法证明1+2+3+…+n2=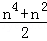
，则当n=k+1时左端应在n=k的基础上加上（）
| A．k2+1 |
| B．（k+1）2 |
C． |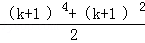
| D．（k2+1）+（k2+2）+（k2+3）+…+（k+1）2 |
用数学归纳法证明：1+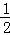
+
+…+
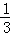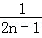＜n（n＞1）．在验证n=2时成立，左式是（）
| A．1 | B．1+ |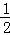
C．1+ + |
D．1+++ |
用数学归纳法证明“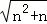
＜n+1 （n∈N*）”．第二步证n=k+1时（n=1已验证，n=k已假设成立），这样证明：
=
＜
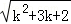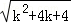=（k+1）+1，所以当n=k+1时，命题正确．此种证法（）
| A．是正确的 |
| B．归纳假设写法不正确 |
| C．从k到k+1推理不严密 |
| D．从k到k+1推理过程未使用归纳假设 |