已知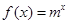 (m为常数,m>0且m≠1).
(m为常数,m>0且m≠1).
设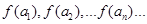 (n∈
(n∈ )是首项为m2,公比为m的等比数列.
)是首项为m2,公比为m的等比数列.
(1)求证:数列 是等差数列;
是等差数列;
(2)若 ,且数列
,且数列 的前n项和为Sn,当m=2时,求Sn;
的前n项和为Sn,当m=2时,求Sn;
(3)若 ,问是否存在m,使得数列
,问是否存在m,使得数列 中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由.
中每一项恒小于它后面的项?若存在,求出m的范围;若不存在,请说明理由.
已知抛物线
(1)
的三个顶点在抛物线
上,记
的三边
、
、
所在的直线的斜率分别为
,
,
若A的坐标在原点,求
的值;
(2)请你给出一个以
为顶点、其余各顶点均为抛物线
上的动点的多边形,写出各多边形各边所在的直线斜率之间的关系式,并说明理由
某甜品店制作蛋筒冰淇淋,其上半部分呈半球形,下半部分呈圆锥形(如图)。现把半径为10cm的圆形蛋皮分成5个扇形,用一个扇形蛋皮围成锥形侧面(蛋皮厚度忽略不计),求该蛋筒冰淇淋的表面积和体积(精确到0.01)

已知向量 ,设函数 ,求函数 的最小正周期及 时的最大值.
某种汽车,购车费用是10万元,每年使用的保险费和汽油费为 万元,年维修费第一年为
万元,年维修费第一年为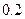 万元,以后逐年递增
万元,以后逐年递增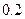 万元,问这种汽车使用多少年时,它的年平均费用最少? (12分)
万元,问这种汽车使用多少年时,它的年平均费用最少? (12分)
在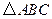 中,内角
中,内角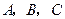 对边的边长分别是
对边的边长分别是 ,且
,且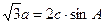 ,
,
(1)求角 (2)若边
(2)若边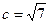 且
且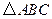 的面积等于
的面积等于 ,求
,求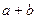 的值.(12分)
的值.(12分)