设函数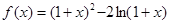
(1)若关于x的不等式 在
在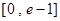 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围;
(2)设 ,若关于x的方程
,若关于x的方程 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
(3)证明不等式: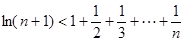

已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数且在定义域内单调递减,求不等式g(x)≤0的解集
函数f(x)是R上的奇函数,且当x>0时,函数的解析式为 .
.
(1)用定义证明f(x)在(0,+∞)上是减函数;
(2)求当x<0时,函数的解析式.
(3)用分段函数形式写出函数f(x)在R上的解析式.当f(a)=3时,求a的值。
用长度为24 m的材料围成一矩形场地,并且中间要用该材料加两道隔墙,要使矩形的面积最大,则隔墙的长度为多少m ?最大面积为多少?
已知集合A={x|-2≤x≤5},B={x|m≤x≤2m-1} A∩B="B," 求m的取值范围。
设a,b∈R,集合{1,a+b,a}=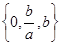 ,求b2010-a2011的值
,求b2010-a2011的值