在某个半径为R=2×106m的行星表面,对于一个质量m0=1kg的砝码,用弹簧称量,其重力大小G0=8N。则:
(1)证明:GM=g0R2(其中,M为该行星的质量,g0为该行星表面的重力加速度。)
(2)求该行星的第一宇宙速度。
(3)若一卫星绕该行星做匀速圆周运动,且测得该卫星绕行N圈所用时间为t,则该卫星离行星表面的高度是多少?(最终结果用R、G0、m0、N、t等字母表述,不必用具体数字代算。)
如图甲是质谱仪的工作原理示意图.图中的A容器中的正离子从狭缝S1以很小的速度进入电压为U的加速电场区(初速度不计)加速后,再通过狭缝S2从小孔G垂直于MN射入偏转磁场,该偏转磁场是以直线MN为上边界、方向垂直于纸面向外的匀强磁场,磁感应强度为B,离子最终到达MN上的H点(图中未画出),测得G、H间的距离为d,粒子的重力可忽略不计。试求:

(1)该粒子的比荷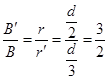
(2)若偏转磁场为半径为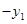 的圆形区域,且与MN相切于G点,如图乙所示,其它条件不变,仍保证上述粒子从G点垂直于MN进入偏转磁场,最终仍然到达MN上的H点,则圆形区域中磁场的磁感应强度
的圆形区域,且与MN相切于G点,如图乙所示,其它条件不变,仍保证上述粒子从G点垂直于MN进入偏转磁场,最终仍然到达MN上的H点,则圆形区域中磁场的磁感应强度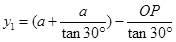 与B之比为多少?
与B之比为多少?
如图所示的电路中,电阻 ,
,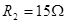 ,电源的电动势E=12V,内电阻r=1Ω,理想电流表A的读数I=0.4A。求:
,电源的电动势E=12V,内电阻r=1Ω,理想电流表A的读数I=0.4A。求:
(1)电阻 的阻值
的阻值
(2)电源的输出功率
(3)电源的效率
竖直放置的两块足够长的平行金属板间有匀强电场.其电场强度为E,在该匀强电场中,用绝缘丝线悬挂质量为m的带电小球,丝线跟竖直方向成θ=30o角时小球恰好平衡,且此时与右板的距离为b,如图所示.已知重力加速度为g,求: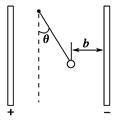
(1)小球带电荷量是多少?
(2)若剪断丝线,小球碰到金属板需多长时间?
如图所示为研究电子枪中电子在电场中运动的简化模型示意图。在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场I和II,已知A、D两点的坐标分别为(L,0)和(-2L,0),两电场的边界均是边长为L的正方形(不计电子所受重力),现在该区域AB边的中点处由静止释放一电子,已知电子质量为m,带电量为e,试求:
(1)电子离开ABCD区域的位置坐标;
(2)电子从电场II出来后经过多少时间到达x轴;
(3)电子到达x轴时的位置坐标。
如图所示电路,已知R2=1Ω,S断开时,两表读数分别为0.5A和2.0V, S闭合时,它们的读数分别变化了0.1A和0.4V,两表均视为理想表,求: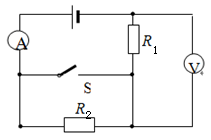
(1)R1的阻值;
(2)电源的电动势和内阻;
(3)S断开时电源的输出功率。