已知函数 .
.
(Ⅰ)当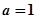 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)若函数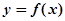 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为 ,问:m在什么范围取值时,对于任意的
,问:m在什么范围取值时,对于任意的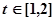 ,函数
,函数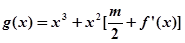 在区间
在区间 上总存在极值?
上总存在极值?
(Ⅲ)当 时,设函数
时,设函数 ,若在区间
,若在区间 上至少存在一个
上至少存在一个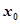 ,使得
,使得 成立,试求实数p的取值范围.
成立,试求实数p的取值范围.
(本小题满分12分) 7名学生按要求排成一排,分别有多少种排法?
(1) 甲乙二人不站在两端;
(2)甲、乙、丙必须相邻;
(3)7名学生中有4男3女,4名男生站在一起,3名女生要站在一起。
(本小题满分10分)
(1)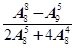
(2)解方程: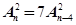
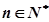
(本小题满分11分)
已知函数 ,
,
(1)求函数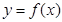 的定义域;
的定义域;
(2)设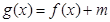 ,若函数
,若函数 在(2,3)内有且仅有一个零点,求实数
在(2,3)内有且仅有一个零点,求实数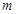 的取值范围;
的取值范围;
(3)设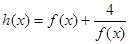 ,求函数
,求函数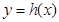 在[3,9]内的值域;
在[3,9]内的值域;
(本小题满分10分)
某电子科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自独立进行为期一个月的技术攻关,同时决定对攻关限期内攻克技术难题的小组给予奖励. 已知此技术难题在攻关期限内被甲小组攻克的概率为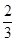 ,被乙小组攻克的概率为
,被乙小组攻克的概率为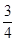 ,
,
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及数学期望
的分布列及数学期望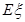 ;
;
(2)设 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数 在定义域内单调递增”为事件C,求事件C发生的概率;
在定义域内单调递增”为事件C,求事件C发生的概率;
(本小题满分9分)
己知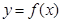 是定义在R上的奇函数,当
是定义在R上的奇函数,当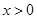 时,
时,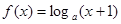 (其中
(其中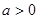 且
且 )
)
(1)求函数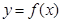 的解析式;
的解析式;
(2)当 为何值时,
为何值时,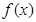 的值的小于0?
的值的小于0?