已知函数 ,其中
,其中 .
.
(Ⅰ)当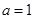 时,求曲线
时,求曲线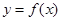 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求 的单调区间.
的单调区间.
受日月引力影响,海水会发生涨退潮现象.通常情况下,船在涨潮时驶进港口,退潮时离开港口.某港口在某季节每天港口水位的深度 (米)是时间
(米)是时间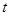 (
(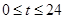 ,单位:小时,
,单位:小时, 表示0:00—零时)的函数,其函数关系式为
表示0:00—零时)的函数,其函数关系式为
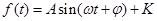
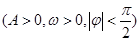 .已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
.已知一天中该港口水位的深度变化有如下规律:出现相邻两次最高水位的深度的时间差为12小时,最高水位的深度为12米,最低水位的深度为6米,每天13:00时港口水位的深度恰为10.5米.
(1)试求函数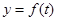 的表达式;
的表达式;
(2)某货船的吃水深度(船底与水面的距离)为7米,安全条例规定船舶航行时船底与海底的距离不小于3.5米是安全的,问该船在当天的什么时间段能够安全进港?若该船欲于当天安全离港,则它最迟应在当天几点以前离开港口?
(本小题满分12分)定义在区间 上的函数
上的函数 的图象关于直线
的图象关于直线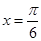 对称,当
对称,当 时函数
时函数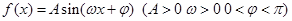 图象如图所示.
图象如图所示.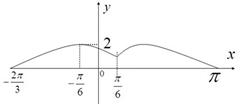
(1)求函数 在
在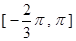 的表达式;
的表达式;
(2)求方程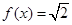 的解;
的解;
(3)是否存在常数 的值,使得
的值,使得 在
在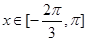 上恒成立;若存在,求出
上恒成立;若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
已知函数 ).
).
(1)求函数 的最小正周期;
的最小正周期;
(2)若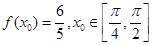 ,求
,求 的值.
的值.
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x= .
.
(1)求φ;
(2)求函数y=f(x)的单调增区间;
(3)画出函数y=f(x)在区间[0,π]上的图象.
在△ABC中,a,b,c分别为内角A,B,C的对边,
且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求sinB+sinC的最大值.