在△ABC中,a,b,c分别为内角A,B,C的对边,
且2asinA=(2b+c)sinB+(2c+b)sinC.
(1)求A的大小;
(2)求sinB+sinC的最大值.
已知函数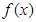 对任意实数
对任意实数 恒有
恒有 且当
且当 时,有
时,有 且
且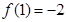 .
.
(1)判断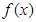 的奇偶性;
的奇偶性;
(2)求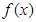 在区间
在区间 上的最大值;
上的最大值;
(3)解关于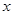 的不等式
的不等式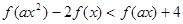 .
.
已知点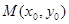 在圆
在圆 上运动,
上运动, ,点
,点 为线段MN的中点.
为线段MN的中点.
(1)求点 的轨迹方程;
的轨迹方程;
(2)求点 到直线
到直线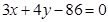 的距离的最大值和最小值..
的距离的最大值和最小值..
如图,四棱锥P-ABCD的底面是矩形,侧面PAD丄底面ABCD,. .
.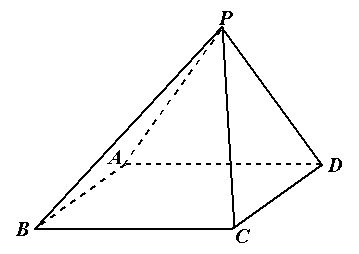
(1)求证:平面PAB丄平面PCD
(2)如果AB=BC=2,PB=PC=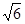 求四棱锥P-ABCD的体积.
求四棱锥P-ABCD的体积.
设直线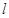 的方程为
的方程为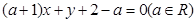 .
.
(1)若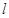 在两坐标轴上的截距相等,求
在两坐标轴上的截距相等,求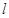 的方程;
的方程;
(2)若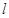 不经过第二象限,求实数
不经过第二象限,求实数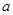 的取值范围。
的取值范围。
已知过曲线 上任意一点
上任意一点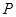 作直线
作直线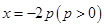 的垂线,垂足为
的垂线,垂足为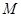 ,且
,且 .
.
⑴求曲线 的方程;
的方程;
⑵设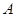 、
、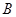 是曲线
是曲线 上两个不同点,直线
上两个不同点,直线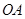 和
和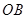 的倾斜角分别为
的倾斜角分别为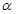 和
和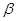 ,当
,当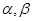 变化且
变化且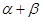 为定值
为定值 时,证明直线
时,证明直线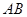 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.