（本小题12分） 如图，在边长为12的正方形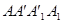
中，点B、C在线段AA′上，且AB=3，BC=4.作BB1∥AA1，分别交A1A1′、AA1′于点B1、P；作CC1∥AA1，分别交A1A1′、AA1′于点C1、Q. 现将该正方形沿BB1，CC1折叠，使得
与AA1重合，构成如图（2）所示的三棱柱ABC-A1B1C1.
（1）在三棱柱ABC-A1B1C1中，求证：AP⊥BC;
（2）在三棱柱ABC-A1B1C1中，连接AQ与A1P，求四面体AA1QP的体积；
（3）在三棱柱ABC- A1B1C1中，求直线 PQ与直线AC所成角的余弦值.
（本小题满分8分）
为了了解某校高一学生体能情况，抽取200位同学进行1分钟跳绳次数测试，将所得数据整理后画出频率分布直方图（如图所示），请回答下列问题：
（1）次数在100~110之间的频率是多少？
（2）若次数在110以上为达标，试估计该校全体高一学生的达标率是多少?
（3）根据频率分布直方图估计，学生跳绳次数的平均数是多少？
（本小题满分6分）
已知
，
，
（1）若
，求实数
的值；
（2）若
，求实数的取值范围。
.(本小题满分10分)
已知圆⊙
,⊙
，过定点
做直线
与大圆⊙
小圆⊙
依次交于
,过点做与直线垂直的直线交小圆于另一点
（如图）.
（Ⅰ）当直线的斜率
时，求
的面积.
（Ⅱ）当直线变化时，求
中点
的轨迹.
(本小题满分9分)
已知
关于
的方程
．
（Ⅰ）若方程
表示圆，求
的取值范围；
（Ⅱ）若圆与直线
相交于
两点，且
，求的值.
. (本小题满分9分)
（如图）在底面为平行四边形的四棱锥
中，
，
平面
，且
，点
是
的中点.
（Ⅰ）求证：
；
（Ⅱ）求证：
平面
；
（Ⅲ）（理科学生做）求二面角
的大小.
（文科学生做）当
，
时，求直线
和平面所成的线面角的大小.