对于数列 ,定义“
,定义“ 变换”:
变换”: 将数列
将数列 变换成数列
变换成数列 ,其中
,其中 ,且
,且 ,这种“
,这种“ 变换”记作
变换”记作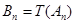 .继续对数列
.继续对数列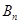 进行“
进行“ 变换”,得到数列
变换”,得到数列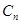 ,…,依此类推,当得到的数列各项均为
,…,依此类推,当得到的数列各项均为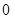 时变换结束.
时变换结束.
(Ⅰ)试问 和
和 经过不断的“
经过不断的“ 变换”能否结束?若能,请依次写出经过“
变换”能否结束?若能,请依次写出经过“ 变换”得到的各数列;若不能,说明理由;
变换”得到的各数列;若不能,说明理由;
(Ⅱ)求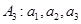 经过有限次“
经过有限次“ 变换”后能够结束的充要条件;
变换”后能够结束的充要条件;
(Ⅲ)证明: 一定能经过有限次“
一定能经过有限次“ 变换”后结束.
变换”后结束.
先化简,再求值: ,其中a=
,其中a= ,b=-
,b=-
解方程: 。
。
计算: 。
。
已知抛物线E1:y=x2经过点A(1,m),以原点为顶点的抛物线E2经过点B(2,2),点A、B关于y 轴的对称点分别为点A′,B′.
(1)求m的值及抛物线E2所表示的二次函数的表达式;
(2)如图1,在第一象限内,抛物线E1上是否存在点Q,使得以点Q、B、B′为顶点的三角形为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由;
(3)如图2,P为第一象限内的抛物线E1上与点A不重合的一点,连接OP并延长与抛物线E2相交于点P′,求△PAA′与△P′BB′的面积之比.
我们把两条中线互相垂直的三角形称为“中垂三角形”.例如图1,图2,图3中,AF,BE是△ABC的中线, AF⊥BE , 垂足为P.像△ABC这样的三角形均为“中垂三角形”.设
 ,
, ,
, .
.
特例探索
(1)如图1,当∠ =45°,
=45°, 时,
时, = ,
= , ;
;
如图2,当∠ =30°,
=30°, 时,
时, = ,
= , ;
;
归纳证明
(2)请你观察(1)中的计算结果,猜想 三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
三者之间的关系,用等式表示出来,并利用图3证明你发现的关系式;
拓展应用
(3)如图4,在□ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG, AD=  ,AB=3.求AF的长.
,AB=3.求AF的长.