(本小题满分14分)
从椭圆 +
+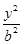 =1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM.
=1(a>b>0)上一点M向x轴作垂线,恰好通过椭圆的左焦点F1,且它的长轴端点A及短轴端点B的连线AB平行于OM.
(Ⅰ)求椭圆的离心率 ;
(Ⅱ)若b=2,设Q是椭圆上任意一点,F2是右焦点,求△F1QF2的面积的最大值;
(Ⅲ)当QF2^AB时,延长QF2与椭圆交于另一点P,若DF1PQ的面积为20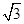 (Q是椭圆上的点),求此椭圆的方程。
(Q是椭圆上的点),求此椭圆的方程。
在平面直角坐标系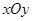 中,椭圆
中,椭圆 的中心为原点,焦点
的中心为原点,焦点 在
在 轴上,离心率为
轴上,离心率为 ,过点
,过点 的直线
的直线 交椭圆
交椭圆 于
于 两点,且
两点,且 的周长为16,求椭圆
的周长为16,求椭圆 的标准方程.
的标准方程.
已知双曲线 :
: 的离心率
的离心率 ,
, 、
、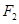 为其左右焦点,点
为其左右焦点,点 在
在 上,且
上,且 ,
, ,
, 是坐标原点.
是坐标原点.
(1)求双曲线 的方程;
的方程;
(2)过 的直线
的直线 与双曲线
与双曲线 交于
交于 两点,求
两点,求 的取值范围.
的取值范围.
袋中有6个球,其中4个白球,2个红球,从袋中任意取出两球,求下列事件的概率:
(1)A:取出的两球都是白球;
(2)B:取出的两球1个是白球,另1个是红球.
如图,在棱长为1的正方体 中,点
中,点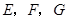 分别是
分别是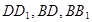 的中点.
的中点.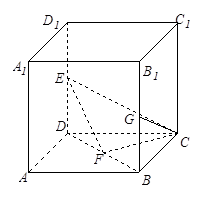
(1)求证: .
.
(2)求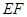 与
与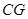 所成角的余弦值.
所成角的余弦值.
20名学生某次数学考试成绩(单位:分)的频率分布直方图如图所示.
(1)求频率分布直方图中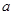 的值;
的值;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数.