某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是 ,样本数据分组为
,样本数据分组为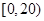 ,
, ,
, ,
, ,
,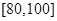 .
.
(Ⅰ)求直方图中 的值;
的值;
(Ⅱ)如果上学所需时间不少于1小时的学生可申请在学校住宿,请估计学校600名新生中有多少名学生可以申请住宿.
(本小题满分15分)已知二次函数 满足条件:①
满足条件:①  ; ②
; ②  的最小值为
的最小值为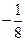 .
.
(1) 求函数 的解析式; (2) 设数列
的解析式; (2) 设数列 的前
的前 项积为
项积为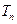 , 且
, 且 , 求数列
, 求数列 的通项公式; (3) 在(2)的条件下, 求数列
的通项公式; (3) 在(2)的条件下, 求数列 的前
的前 项的和.
项的和.
(本小题满分15分)已知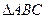 的面积
的面积 满足
满足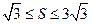 ,且
,且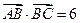 .
.
(1)求角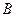 的取值范围;(2)求函数
的取值范围;(2)求函数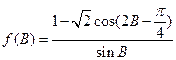 的值域.
的值域.
(本小题满分14分)已知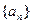 的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且
的首项为a1,公比q为正数(q≠1)的等比数列,其前n项和为Sn,且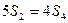 .(1)求q的值;(2)设
.(1)求q的值;(2)设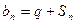 ,请判断数列
,请判断数列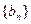 能否为等比数列,若能,请求出a1的值,否则请说明理由.
能否为等比数列,若能,请求出a1的值,否则请说明理由.
(本小题满分14分)已知全集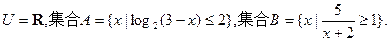
(1)求A、B;(2)求
(本小题满分14分)已知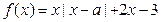 (Ⅰ)当
(Ⅰ)当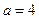 ,
,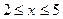 时,问
时,问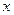 分别取何值时,函数
分别取何值时,函数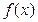 取得最大值和最小值,并求出相应的最大值和最小值;(Ⅱ)若
取得最大值和最小值,并求出相应的最大值和最小值;(Ⅱ)若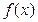 在R上恒为增函数,试求
在R上恒为增函数,试求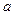 的取值范围;
的取值范围;
(Ⅲ)已知常数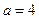 ,数列
,数列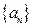 满足
满足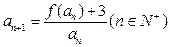 ,试探求
,试探求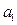 的值,使得数列
的值,使得数列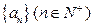 成等差数列.
成等差数列.