已知菱形ABCD中，AB=4，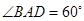 
（如图1所示），将菱形ABCD沿对角线
翻折，使点
翻折到点
的位置（如图2所示），点E，F，M分别是AB，DC1，BC1的中点．
（Ⅰ）证明：BD //平面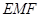
；
（Ⅱ）证明：
；
（Ⅲ）当
时，求线段AC1的长．
命题p：∀x∈(1，＋∞)，函数f(x)＝|log2x|的值域为[0，＋∞)；命题q：∃m≥0，使得y＝sin mx的周期小于
，试判断p∨q，p∧q，
p的真假性．
已知集合A＝{x|x2－4mx＋2m＋6＝0}，B＝{x|x<0}，若命题“A∩B＝∅”是假命题，求实数m的取值范围．
已知集合A＝
，B＝{x|x＋m2≥1}．若“x∈A”是“x∈B”的充分条件，求实数m的取值范围．
已知集合A＝
，B＝{x|m＋1≤x≤2m－1}．
(1)求集合A；
(2)若B⊆A，求实数m的取值范围．
设集合A＝{x|x2＋2x－3＞0}，B＝{x|x2－2ax－1≤0，a＞0}．若A∩B中恰含有一个整数，求实数a的取值范围．