如图所示，在直角坐标系xOy平面内有一矩形区域MNPQ，矩形区域内有水平向右的匀强电场，场强为E；在y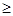
0的区域内有垂直于坐标平面向里的匀强磁场，半径为R的光滑绝缘空心半圆管ADO固定在坐标平面内，半圆管的一半处于电场中，圆心O1为MN的中点，直径AO垂直于水平虚线MN，一质量为m、电荷量为q的带电粒子（重力不计）从半圆管的O点由静止释放，进入管内后从A点穿出恰能在磁场中做半径为R的匀速圆周运动，当粒子再次进入矩形区域MNPQ时立即撤去磁场，此后粒子恰好从QP的中点C离开电场。求
（1）匀强磁场的磁感应强度B的大小；
（2）矩形区域的长度MN和宽度MQ应满足的条件？
（3）粒子从A点运动到C点的时间。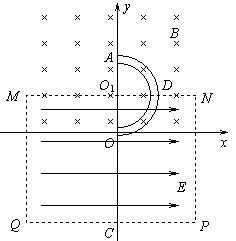
如图所示，在竖直平面内，由倾斜轨道AB、水平轨道BC和半圆形轨道CD连接而成的光滑轨道，AB与BC的连接处是半径很小的圆弧，BC与CD相切，圆形轨道CD的半径为R。质量为m的小物块从倾斜轨道上距水平面高为h=3R处由静止开始下滑。求：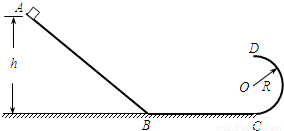
（1）小物块通过B点时速度vB的大小；
（2）试通过计算说明，小物块能否通过圆形轨道的最高点D。
如图所示，用恒力F使一个质量为m的物体由静止开始沿水平地面移动了位移x，力F跟物体前进的方向的夹角为α，物体与地面间的动摩擦因数为μ，求：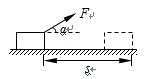
（1）拉力F对物体做功W的大小；
（2）物体获得的动能Ek。
纯电动概念车E1是中国馆的镇馆之宝之一。若E1概念车的总质量为920kg，在16s内从静止加速到100km/h（即27.8m/s），受到恒定的阻力为1500N，假设它做匀加速直线运动，求：
（1）动力系统提供的牵引力为多少？
（2）当E1概念车以最高时速120km/h（即33.3m/s）做匀速直线运动时，其动力系统输出的功率为多少？
如图所示，斜面和水平面由一小段光滑圆弧连接，斜面的倾角为37°，一质量为0.5kg的物块从斜面上距斜面底端B点5m处的A点由静止释放．已知物块与水平面和斜面的动摩擦因数均为0.3（sin37°=0.6，cos37°=0.8，g=10m/ s2）
（1）物块在水平面上滑行的时间为多少？
（2）若物块开始静止在水平面上距B点10m 的C点处，用大小为4.5N的水平恒力向右拉该物块，到B点撤去此力，物块第一次到A点时的速度为多大？
（3）若物块开始静止在水平面上距B点10m 的C点处，用大小为4.5N的水平恒力向右拉该物块，欲使物块能到达A点，水平恒力作用的最短距离为多大？
如图所示，为拔桩装置，当用力大小为F且方向垂直向下的作用力拉图中E点时，绳CE被水平拉直，绳CA被拉为竖直，绳DE与水平方向夹角为α，绳BC与竖直方向的夹角为β，求绳CA拔桩的作用力的大小。