如图所示,一细光束以60°的入射角从空气射向长方体透明玻璃砖ABCD的上表面E点,折射光线恰好过C点,已知BC=30cm,BE=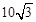 cm,求
cm,求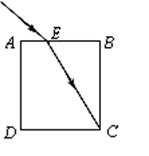
①此玻璃砖的折射率;
②光束在玻璃砖中传播的时间。
如图所示,长为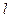 的绳子下端连着质量为m的小球,上端悬于天花板上,当把绳子拉直时,绳子与竖直线夹角为600,此时小球静止于光滑水平桌面上。
的绳子下端连着质量为m的小球,上端悬于天花板上,当把绳子拉直时,绳子与竖直线夹角为600,此时小球静止于光滑水平桌面上。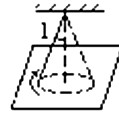
(1)当球以w=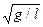 做圆锥摆运动时,绳子张力T为多大
做圆锥摆运动时,绳子张力T为多大 ?桌面受到压力N为多大?
?桌面受到压力N为多大?
(2)当球以角速度w=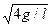 做圆锥摆运动时,绳子的张力及桌面受到的压力各为多少?
做圆锥摆运动时,绳子的张力及桌面受到的压力各为多少?
利用航天飞机,人们可以到太空维修出现故障的人造地球卫星。已知一颗人造地球卫星在离地高度一定的圆轨道上运行。当航天飞机接近这颗卫星并与它运行情况基本相同时,速度达到了6.4km/s。取地球半径为R = 6400km, 地球表面的重力加速度为g = 9.8m/s2,试求这颗卫星离地面的高度。(结果保留2位有效数字)
地球表面的重力加速度为g = 9.8m/s2,试求这颗卫星离地面的高度。(结果保留2位有效数字)
某滑板爱好者在离地h=1.8m高的平台上滑行,水平离开A点后落在水平地面的B点,其水平位移s1=3m.着地时由于存在能量损失,着地后速度变为v=4m/s,并以此为初速沿水平地面滑行s2=8m后停止.已知人与滑板的 总质量m=60kg
总质量m=60kg .求:
.求: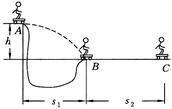
(1)人与滑板在水平地面滑行时受到的平均阻力大小;
(2)人与滑板离开平台时的水平初速度.(空气阻力忽略不计,g=10m/s2)
质量为2kg的物体置于水平地面上,用10N的水平拉力使它从静止开始作直线运动,第3s末速度为6m/s,此时撤去拉力,试求:
⑴ 撤去拉力瞬间物体的动能?
⑵ 撤去拉力前拉力做了多少功?
⑶ 撤去拉力后物体克服摩擦力所做多少功 ?
1)为了清理堵塞河道的冰凌,空军实施了投弹爆破,飞机在河道上空高H处以速度v0水平匀速飞行,投掷下炸弹并击中目标。求炸弹刚脱离飞机到击中目标所飞行的水平距离及击中目标时的速度大小。(不计空气阻力)
(2)如图17所示,一个竖直放置的圆锥筒可绕其中心OO′转动,筒内壁粗糙,筒口半径和筒高分别为R和H,筒内壁A点的高度为筒高的一半。内壁上有一质量为m的小物块。求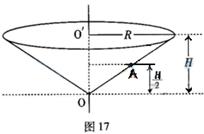
①当筒不转动时,物块静止在筒壁A点受到的摩擦力和支持力的大小;
②当物块在A点随筒做匀速转动,且其受到的摩擦力为零时,筒转动的 角速度。