某学生想了解所居住高楼内电梯运行的大致规律，他设计一个利用称体重的磅秤来进行测量和研究的方案：
①把磅秤平放在电梯的地板上，他站在磅秤上，请两位同学协助他观察磅秤示数的变化情况，并记录电梯运行时不同时刻磅秤的示数．
②将两位同学随机记录的7个数据列表．由于不知记录时刻的先后，故表格数据按从小到大的次序排列，并相应标明t1、t2……t7．（记录时电梯作平稳运动）
③对实验数据进行分析研究，了解电梯的运行情况，并粗略测 定电梯的加速度．
思考回答下列问题：
1. 在测量时该学生所受的重力将____________（填“变大”、“变小”、“不变”）
2．如果先记录到的是较小的示数，后记录到的是较大的示数，则记录时电梯相应的运动可能是 ［ ］
A. 先加速下降后减速下降 B．先减速下降后匀速下降
C．先匀速上升后减速上升 D．先减速上升后加速上升
3．如果电梯在运行过程中经历过匀加速、匀速和匀减速三个过程，而两位同学记录的数据不知处于哪一运动阶段，则此电梯加速度的可能值为
A．1.0m/s2 B．1.82m/s2 C．2.22m/s2 D．2.50m/s2 ［ ］
4. 由于每部电梯运行时加速度都是设定好的，如果要知道该高楼电梯的加速度，还需要测定的物理量是__________________________．
宇宙飞船进入靠近某行星表面的圆形轨道，绕行数圈后着陆在该行星上，宇航员在绕行及着陆后各做一次测量，依据所测量的数据，可以求出该行星的质量M、半径R（已知引力常量为G）. 如果宇宙飞船上备有的实验仪器有：
| A．一只秒表 |
| B．一个弹簧秤 |
| C．一个质量为m的钩码 |
| D．一把毫米刻度尺 |
（1）宇航员两次测量所选用的仪器分别是__________和___________.
（2）宇航员两次测量的物理量分别是___________和___________.
（3）用测得的数据求得该行星的半径R＝___________，质量M___________.
一个同学在《研究平抛物体的运动》实验中，只画出了如图9所示的一部分曲线，于是他在曲线上取水平距离
相等的三点A、B、C，量得= 0.2m。又量出它们之间的竖直距离分别为h1 = 0.1m，h2 = 0.2m，利用这些数据，可求得：
（1）物体抛出时的初速度为m/s；
（2）物体经过B时竖直分速度为m/s；
（3）抛出点在A点上方高度为m处。
发射地球同步卫星时，先将卫星发射至近地圆轨道1，然后经点火，使其沿椭圆轨道2运行，最后再次点火，将卫星送人同步圆轨道3，轨道1、2相切于Q点，轨道2、3相切于P点.如图所示,则卫星分别在1、2、3轨道上运行时，以下说法正确的是( )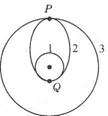
| A．卫星在轨道3上的速率大于在轨道1上的速率 |
| B．卫星在轨道3上的角速度小于在轨道1上的角速度 |
| C．卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度 |
| D．卫星在轨道2上经过P点的加速度等于它在轨道3上经过P点时的加速度 |
A、B两球在光滑水平面上沿一直线相向运动，已知B球的质量是A球质量的4倍，碰撞前A球速度大小为vA=v，B球速度大小vB=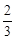
v，若碰后B球速度减小为
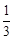v但方向不变，则碰撞前后系统的总动量_______（选填“不变”、“增大”或“减小”），碰后A球的速度大小vA=____．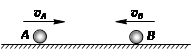
在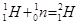 
的核反应中，要（填“吸收”或“放出”）2.22 Mev的能量，核反应过程中的质量亏损为kg．（保留两位有效数字）