[本小题满分12分]
为了了解小学生的体能情况，抽取了某小学同年级部分学生进行跳绳测试，将所得的数据整理后画出频率分布直方图（如下图），已知图中从左到右的前三个小组的频率分别是0.1，0.3，0.4.第一小组的频数是5.
(1) 求第四小组的频率和参加这次测试的学生人数；
(2) 在这次测试中，学生跳绳次数的中位数落在第几小组内？
(3) 参加这次测试跳绳次数在100次以上为优秀，估计该校此年级跳绳成绩优秀率是多少？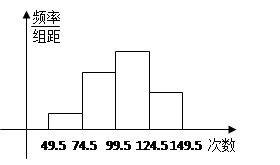
已知函数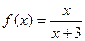
，数列
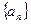满足
，
（1）求数列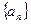的通项公式
；
（2）若数列
满足
，求
在一次语文测试中，有一道把我国近期新书:《声涯》、《关于上班这件事》、《长尾理论》、《游园惊梦:昆曲艺术审美之旅》与它们的作者连线题，已知连对一个得3分，连错一个不得分，一位同学该题得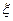
分.
（1）求该同学得分不少于6分的概率；
（2）求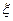的分布列及数学期望.
已知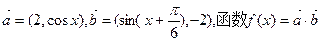
.
（1）求函数
的单调增区间；
（2）若
的值
已知一条曲线C在y轴右边，C上每一点到点F（1，0）的距离减去它到y轴距离的差都是1.
（1）求曲线C的方程；
（2）是否存在正数m, 对于过点M（m,0）且与曲线C有两个交点A,B的任一直线，都有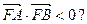
若存在，求出m的取值范围；若不存在，请说明理由。
已知双曲线
的离心率为2，焦点到渐近线的距离为
，点P的坐标为（0，－2），过P的直线l与双曲线C交于不同两点M、N.
（1）求双曲线C的方程；
（2）设
（O为坐标原点），求t的取值范围