质量为M,电阻为R的薄金属条制成边长为L的闭合正方形框abb´a´。如图所示,金属方框水平放在磁极的狭缝间,方框平面与磁场方向平行。设匀强磁场仅存在于相对磁极之间,其他地方的磁场忽略不计。可认为方框的aa´边和bb´边都处在磁极间,极间磁感应强度大小为B。方框从静止开始释放,其平面在下落过程中保持水平(不计空气阻力)

(1)求方框下落的最大速度vm(设磁场区域在竖直方向足够长);
(2)当方框下落的加速度为g/2时,求方框的发热功率P;
(3)已知方框下落的时间为t时,下落的高度为h,其速度为vt(vt<vm)。求此过程中方框中产生的热量。(根据能量守恒定律)
(4)若在同一时间t内,方框内产生的热与一恒定电流I0在该框内产生的热相同,求恒定电流I0的表达式。
如图所示,A、B为真空中相距为d的一对平金属板,两板间的电压为U,一电子以v0的速度从带负电A板小孔与板面垂直地射入电场中.已知电子的质量为m,电子的电荷量为e.求:
(1)电子从B板小孔射出时的速度大小;
(2)电子离开电场时所需要的时间.
如图所示,R1=14Ω R2=9Ω.当开关处于位置1时,电流表读数I1=0.2A;当开关处于位置2时,电流表的读数I2=0.3A.求电源的电动势E和内电阻r.
如图所示,半径为r=10cm、质量为M=1.8kg的均匀球靠竖直墙放置,左下方有一厚为h=4cm、质量为m=1kg的木块.(取g=10m/s2)
(1)若不计摩擦.用多大的水平力F推木块才能使球恰好离开地面?
(2)此时木块对地的压力?
在倾角为37°的斜面上放着一个质量M=2kg的物体A,由轻绳与质量为m的物体B相连,物体A与斜面的动摩擦因数μ=0.5.如图所示,A和B都处于静止状态,求B物体的质量.(g取10N/kg,最大静摩擦力等于滑动摩擦力)
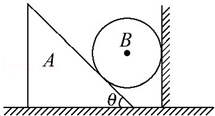
如图所示,斜面体A放在水平地面上,斜面倾角为θ.质量为m的光滑球B放在斜面体和光滑竖直墙壁之间,A和B都处于静止状态,求地面对斜面体的摩擦力.