如图,在△ABC中,AB=AC,BD、CE分别是两腰上的高,且BD、CE相交于O,
(1)请你写出三类不同的正确的结论
(2)设∠CBD=α,∠A=β,试找出α与β之间的一种关系等式,并给予适当的说明(友情提示:∠ABC=∠ACB)
如图,AC=AE,∠1=∠2,AB=AD.
求证:BC=DE.
求x的值与计算
(1)4x2=81
(2)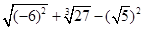
如图,在直角坐标系中,已知P(-2,-1),点T(t,0)是x轴上的一个动点.
(1)求点P关于原点的对称点M的坐标.
(2)已知点N(0,2)为y轴上的一点,求经过P、M、N三点的抛物线的解析式,并求出该抛物线的顶点坐标.
(3)点T在运动过程中,是否存在某个时刻使△MTO为等腰三角形?若存在,求出点T的坐标.若不存在,请说明理由.
在平行四边形ABCD中,过点D作DE⊥AB与点E,点F在边CD上,DF=BE,连接AF、BF.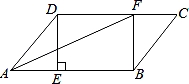
(1)求证:四边形BFDE是矩形.
(2)若CF=3,BF=4,DF=5,求证:△ADF是等腰三角形.
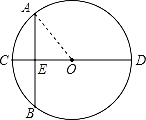
“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题,“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图所示,CD为⊙O的直径,CD⊥AB,垂足为E,CE=1寸,AB=1尺,求直径CD长是多少寸?”(注:1尺=10寸)