“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题,“今有圆材,埋壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现在的数学语言表述是:“如图所示,CD为⊙O的直径,CD⊥AB,垂足为E,CE=1寸,AB=1尺,求直径CD长是多少寸?”(注:1尺=10寸)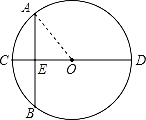
计算:6cos45°-|4- |+
|+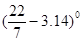 +(-
+(-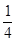 )-1
)-1
如图1,已知抛物线y=-x2+bx+c经过点A(1,0),B(-3,0)两点,且与y轴交于点C.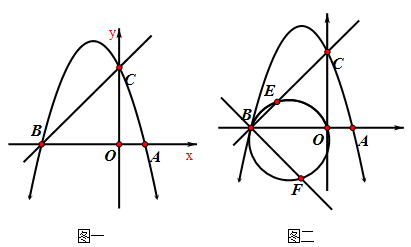
(1)求b,c的值.
(2)在第二象限的抛物线上,是否存在一点P,使得△PBC的面积最大?求出点P的坐标及△PBC的面积最大值. 若不存在,请说明理由.
(3)如图2,点E为线段BC上一个动点(不与B,C重合),经过B、E、O三点的圆与过点B且垂直于BC的直线交于点F,当△OEF面积取得最小值时,求点E坐标.
阅读材料:用配方法求最值.已知x,y为非负实数,
∵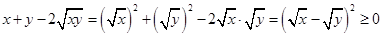
∴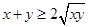 ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立.
示例:当x>0时,求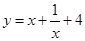 的最小值.
的最小值.
解: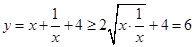 ,当
,当 ,即x=1时,y的最小值为6.
,即x=1时,y的最小值为6.
(1)尝试:当x>0时,求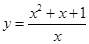 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养、维护费用总和为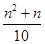 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用= )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
如图,△ABC中,AC=BC,以BC上一点O为圆心,OB为半径作⊙O交AB于点D已知经过点D的⊙O切线恰好经过点C
(1)试判断CD与AC的位置关系,并证明;
(2)若△ACB∽△CDB,且AC=3,求图中阴影部分的面积
如图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A、B之间的距离是多少?(结果精确到1米.参考数据:sin32°=0.5299,cos32°=0.8480)