阅读材料:用配方法求最值.已知x,y为非负实数,
∵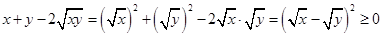
∴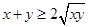 ,当且仅当“x=y”时,等号成立.
,当且仅当“x=y”时,等号成立.
示例:当x>0时,求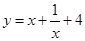 的最小值.
的最小值.
解: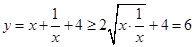 ,当
,当 ,即x=1时,y的最小值为6.
,即x=1时,y的最小值为6.
(1)尝试:当x>0时,求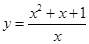 的最小值.
的最小值.
(2)问题解决:随着人们生活水平的快速提高,小轿车已成为越来越多家庭的交通工具,假设某种小轿车的购车费用为10万元,每年应缴保险费等各类费用共计0.4万元,n年的保养、维护费用总和为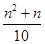 万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用=
万元.问这种小轿车使用多少年报废最合算(即:使用多少年的年平均费用最少,年平均费用= )?最少年平均费用为多少万元?
)?最少年平均费用为多少万元?
如图,已知AB为⊙O的直径,PA与⊙O相切于点A,线段OP与弦AC垂直并相交于点D,OP与⊙O相交于点E,连接BC.
(1)求证:△PAD∽△ABC;
(2)若PA=10,AD=6,求AB的长.
如图,某校数学兴趣小组的同学欲测量祁阳县文昌古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退12米至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度(结果保留根号).
已知:如图,在平面直角坐标系 中,直线AB分别与
中,直线AB分别与 轴交于点B、A,与反比例函数的图象分别交于点C、D,
轴交于点B、A,与反比例函数的图象分别交于点C、D, 轴于点E,
轴于点E,

 .求该反比例函数的解析式.
.求该反比例函数的解析式.
如图,⊙O是△ 的外接圆,
的外接圆, ,
, 为⊙O的直径,且
为⊙O的直径,且 ,连结
,连结 ,求BC的长.
,求BC的长.
某校准备选出甲、乙两人中的一人参加县里的射击比赛,他们在相同条件下各射靶5次,成绩统计如下:
| 命中环数/环 |
7 |
8 |
9 |
10 |
| 甲命中的频数/次 |
1 |
1 |
0 |
3 |
| 乙命中的频数/次 |
0 |
1 |
3 |
1 |
(1)求甲、乙两人射击成绩的方差分别是多少?
(2)已知该校选手前三年都取得了县射击比赛的第一名,请问应选择谁去参加比赛?