如图所示,一块涂有炭黑玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上运动。一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃板上画出了图示曲线,量得 OA=1cm,OB=4cm,OC=9cm.求外力F的大小。(g=10m/s2,不计阻力)
如图所示,两根相同的平行金属直轨道竖直放置,上端用导线接一定值电阻,下端固定在水平绝缘底座上。底座中央固定一根弹簧,金属直杆ab通过金属滑环套在轨道上。在MNPQ之间分布着垂直轨道面向里的匀强磁场,现用力压杆使弹簧处于压缩状态,撤力后杆被弹起,脱离弹簧后进入磁场,穿过PQ后继续上升,然后再返回磁场,并能从边界MN穿出,此后不再进入磁场。杆ab与轨道的摩擦力大小恒等于杆重力的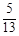 倍。已知杆向上运动时,刚穿过PQ时的速度是刚穿过MN时速度的一半,杆从PQ上升的最大高度(未超过轨道上端)是磁场高度的n倍;杆向下运动时,一进入磁场立即做匀速直线运动。除定值电阻外不计其它一切电阻,已知重力加速度为g。求:
倍。已知杆向上运动时,刚穿过PQ时的速度是刚穿过MN时速度的一半,杆从PQ上升的最大高度(未超过轨道上端)是磁场高度的n倍;杆向下运动时,一进入磁场立即做匀速直线运动。除定值电阻外不计其它一切电阻,已知重力加速度为g。求:
(1)杆向上穿过PQ时的速度与返回PQ时的速度大小之比v1:v2;
(2)杆向上运动刚进入MN时的加速度大小a;
(3)杆向上、向下两次穿越磁场的过程中产生的电热之比Q1:Q2。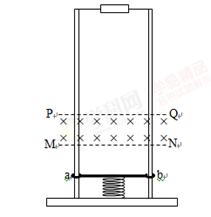
如甲图所示,长为4m的水平轨道AB与倾角为37°的足够长斜面BC在B处平滑连接,有一质量为2kg的滑块,从A处由静止开始受水平向右的力F作用,F与位移x的关系按乙图所示规律变化,滑块与AB和BC间的动摩擦因数均为0.5,重力加速度g取l0m/s2。求:
(1)滑块第一次到达B处时的速度大小;
(2)不计滑块在B处的速率变化,滑块到达B点时撤去力F,滑块冲上斜面,则滑块最终静止的位置与B点的距离多大。(sin37°=0.6)
在光滑的水平面上,一质量为mA=0.1kg的小球A,以8 m/s的初速度向右运动,与质量为mB=0.2kg的静止小球B发生弹性正碰。碰后小球B滑向与水平面相切、半径为R=0.5m的竖直放置的光滑半圆形轨道,且恰好能通过最高点N后水平抛出。g=10m/s2。求: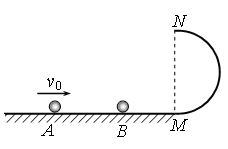
(1) 碰撞后小球B的速度大小;
(2) 小球B从轨道最低点M运动到最高点N的过程中所受合外力的冲量;
(3) 碰撞过程中系统的机械能损失。
有频率相同、振动方向相同的两个声源S1和S2,如图所示.一人站在声源北方的A点,此人此时听到的声音很响,这个人向东慢慢移动,声音逐渐减弱,到B点时几乎听不到声音,测得A、B间距离为1.5 m.则: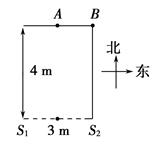
①S1、S2声波的波长λ为多少?
②若此人由B点再向正南方向移动,声音逐渐变响,那么,此人沿正南方向至少走多远,声音又变得很响?
如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1 =" 0.40" T,方向垂直纸面向里,电场强度E = 2.0×105 V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有垂直纸面的正三角形匀强磁场区域(图中未画出),磁感应强度B2 =" 0.25" T。一束带电量q = 8.0×10-19 C,质量m = 8.0×10-26 kg的正离子从P点射入平行板间,不计重力,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射向三角形磁场区,离子通过x轴时的速度方向与x轴正方向夹角为60°。则: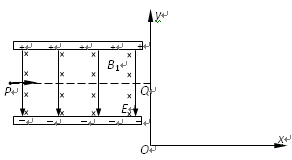
(1)离子运动的速度为多大?
(2)若正三角形区域内的匀强磁场方向垂直纸面向外,离子在磁场中运动的时间是多少?
(3)若正三角形区域内的匀强磁场方向垂直纸面向里,正三角形磁场区域的最小边长为多少?
(4)第(3)问中离子出磁场后经多长时间到达X轴?