(Ⅰ)在等差数列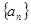 中,
中,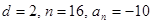 ,求
,求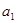 及
及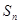 ;
;
(Ⅱ)在等比数列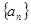 中,已知
中,已知 ,
,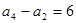 ,求
,求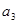 。
。
某化工厂生产一种溶液,按市场要求,杂质含量不超过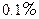 ,若初时含杂质
,若初时含杂质 ,每过滤一次可使杂质含量减少
,每过滤一次可使杂质含量减少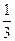 ,问至少应过滤几次才能使产品达到市场要求?(已知
,问至少应过滤几次才能使产品达到市场要求?(已知 )
)
某工厂生产一种机器的固定成本(即固定投入)为0.5万元,但每生产一台,需要增加可变成本(即另增加投入)0.25万元.市场对此产品的年需求量为500台.销售的收入函数为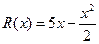 (万元)
(万元)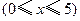 ,其中
,其中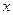 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).
(1)把利润表示为年产量的函数;
(2)年产量是多少时,工厂所得利润最大?
(3)年产量是多少时,工厂才不亏本?
某地为促进淡水鱼养殖业的发展,将价格控制在适当范围内,决定对淡水鱼养殖提供政府补贴.设淡水鱼的市场价格为 元/千克,政府补贴为
元/千克,政府补贴为 元/千克.根据市场调查,当
元/千克.根据市场调查,当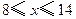 时,淡水鱼的市场日供产量
时,淡水鱼的市场日供产量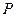 千克与市场日需求量
千克与市场日需求量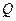 千克近似地满足关系:
千克近似地满足关系: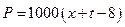 ,
,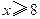 ,
,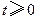 ,
,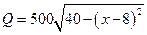 ,
,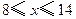 .
.
当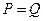 时的市场价格称为市场平衡价格.
时的市场价格称为市场平衡价格.
(1)将市场平衡价格表示为政府补贴的函数,并求出函数的定义域;
(2)为使市场平衡价格不高于每千克10元,政府补贴至少为每千克多少元?
已知 ,
,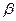 分别是关于
分别是关于 的方程
的方程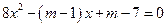 的两个根,且
的两个根,且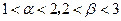 ,求实数
,求实数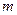 的取值范围.
的取值范围.
某公司为了实现1000万元利润的目标,准备制定一个激励销售部门的奖励方案;在销售利润达到10万元时,按销售利润进行奖励,且奖金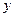 (单位:万元)随销售利润
(单位:万元)随销售利润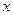 (单位:万元)的增加而增加,但奖金总数不超过
(单位:万元)的增加而增加,但奖金总数不超过 万元,同时奖金不超过利润的
万元,同时奖金不超过利润的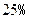 .现有三个奖励模型:
.现有三个奖励模型: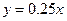 ,
,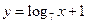 ,
,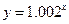 .其中哪个模型能符合公司的要求?
.其中哪个模型能符合公司的要求?