某工厂生产一种机器的固定成本(即固定投入)为0.5万元,但每生产一台,需要增加可变成本(即另增加投入)0.25万元.市场对此产品的年需求量为500台.销售的收入函数为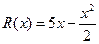 (万元)
(万元)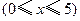 ,其中
,其中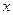 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).
(1) 把利润表示为年产量的函数;
(2) 年产量是多少时,工厂所得利润最大?
(3) 年产量是多少时,工厂才不亏本?
随着机构改革工作的深入进行,各单位要减员增效。有一家公司现有职员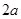 人,(
人,( ,且
,且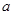 为偶数),每人每年可创利
为偶数),每人每年可创利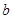 万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利
万元。据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年可多创利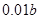 万元,但公司需支付下岗职员每人每年
万元,但公司需支付下岗职员每人每年 万元的生活费,并且该公司正常运转所需人数不得小于现有员工的
万元的生活费,并且该公司正常运转所需人数不得小于现有员工的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无法确认,在图中以X表示.
(1)如果X=8,求乙组同学植树棵数的平均数和方差;
(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.
(注:方差s2= [(x1-
[(x1-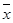 )2+(x2-
)2+(x2-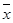 )2+…+(xn-
)2+…+(xn-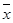 )2]),其中
)2]),其中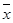 为x1,x2,…,xn的平均数)
为x1,x2,…,xn的平均数)
以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据:
| 房屋面积(m2) |
115 |
110 |
80 |
135 |
105 |
| 销售价格(万元) |
24.8 |
21.6 |
18.4 |
29.2 |
22 |
(1)画出数据对应的散点图;
(2)求线性回归方程,并在散点图中加上回归直线;
(3)根据(2)的结果估计当房屋面积为150 m2时的销售价格.
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
某市2010年4月1日—4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
(1)完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.