(本题11分)如图所示,矩形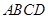 中,
中,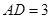 厘米,
厘米, 厘米(
厘米(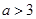 ).动点
).动点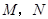 同时从
同时从 点出发,分别沿
点出发,分别沿 ,
,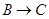 运动,速度是
运动,速度是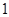 厘米/秒.过
厘米/秒.过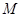 作直线垂直于
作直线垂直于 ,分别交
,分别交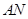 ,
, 于
于 .当点
.当点 到达终点
到达终点 时,点
时,点 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为 秒.
秒.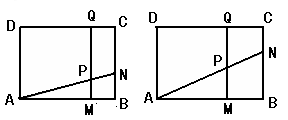
(1)若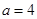 厘米,
厘米, 秒,求PM的长度;
秒,求PM的长度;
(2)若 厘米,求出某个时间
厘米,求出某个时间 ,使⊿PNB∽⊿PAD,并求出它们的相似比;
,使⊿PNB∽⊿PAD,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求 的取值范围;
的取值范围;
(本小题满分11分)
如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.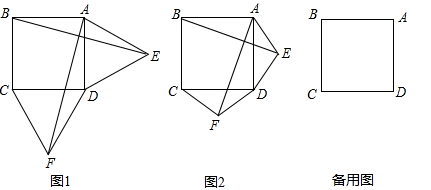
(1)请判断:AF与BE的数量关系是 ,位置关系是 ;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
(本小题满分10分)如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形.其中线段BD交AC于点G,线段AE交CD于点F.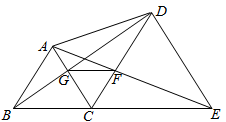
求证:(1)△ACE≌△BCD;
(2)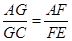 .
.
((本小题满分6分)
小颖和小丽做“摸球”游戏:在一个不透明的袋子中装有编号为1~4的四个球(除编号外都相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字。若两次数字之和大于5,则小颖胜,否则小丽胜。这个游戏对双方公平吗?请说明理由。
(本小题满分6分)
某小学为了解学生每天完成家庭作业所用时间的情况,从每班抽取相同数量的学生进行调查,并将所得数据进行整理,制成条形统计图和扇形统计图如下: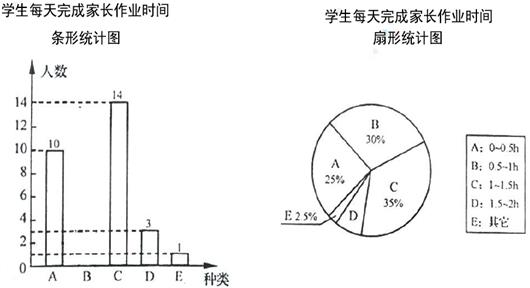
(1)补全条形统计图;
(2)求扇形统计图中扇形D的圆心角的度数;
(3)若该中学有2000名学生,请估计其中有多少名学生能在1.5小时内完成家庭作业?
根据某网站调查,2014年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其他共五类.根据调查的部分相关数据,绘制的统计图表如下:
根据所给信息解答下列问题:
(1)请补全条形统计图并在图中标明相应数据;
(2)若菏泽市约有880万人口,请你估计最关注环保问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,试用列表或树形图的方法求抽取的两人恰好是甲和乙的概率.