已知函数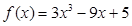 .
.
(Ⅰ)求函数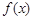 的单调递增区间;
的单调递增区间;
(Ⅱ)求函数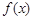 在
在 的最大值和最小值.
的最大值和最小值.
已知函数
(Ⅰ)若 有两个极值点,求实数
有两个极值点,求实数 的取值范围;
的取值范围;
(Ⅱ)当 时,讨论函数
时,讨论函数 的零点个数.
的零点个数.
设数列 满足
满足 .
.
(Ⅰ)求 ,并由此猜想
,并由此猜想 的一个通项公式,证明你的结论;
的一个通项公式,证明你的结论;
(II)若 ,不等式
,不等式 对一切
对一切 都成立,求正整数m的最大值。
都成立,求正整数m的最大值。
已知函数 .
.
(I)若 ,求
,求 在
在 处的切线方程;
处的切线方程;
(II)求 在区间
在区间 上的最小值.
上的最小值.
盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分 . 现从盒内任取3个球
(Ⅰ)求取出的3个球中至少有一个红球的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求 的分布列.
的分布列.
已知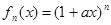 ,且
,且 展开式的各式系数和为243.
展开式的各式系数和为243.
(I)求a的值。
(II)若 ,求
,求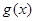 中含
中含 的系数。
的系数。