(本题满分14分)数列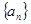 中,
中,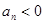 , 前n项和
, 前n项和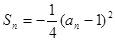 .
.
(1)求数列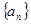 的通项公式;
的通项公式;
(2)设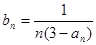 (
(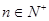 ),
),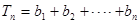 ,若对任意
,若对任意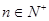 ,总存在
,总存在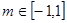 使
使 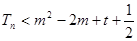 成立,求出t的取值范围.
成立,求出t的取值范围.
等差数列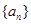 的各项均为正数,
的各项均为正数, ,前
,前 项和为
项和为 ,
,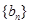 为等比数列,
为等比数列,  ,
,
且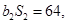
 .
.
(Ⅰ)求 与
与 ;
;
(Ⅱ)求和: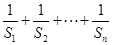 .
.
袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分为1,2.
(Ⅰ)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(Ⅱ)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
已知一圆经过点A(2,-3)和B(-2,-5),且圆心C在直线l: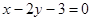 ,此圆的标准方程.
,此圆的标准方程.
设函数f(x)=4x3+ax2+bx+5在x=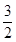 与x=-1时有极值.
与x=-1时有极值.
(1)写出函数的解析式;
(2)指出函数的单调区间;
(3)求f(x)在[-1,2]上的最大值和最小值.
从参加高一年级迎新数学竞赛的学生中,随机抽取了 名学生的成绩进行统计分析.
名学生的成绩进行统计分析.
(1)完成下列频率分布表,并画出频率分布直方图;
(2)从成绩是[50,60)和[90,100)的学生中选两人,求他们在同一分数段的概率.
| 分 组 |
频数 |
频率 |
 |
2 |
|
 |
10 |
|
 |
20 |
|
 |
15 |
|
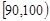 |
3 |
|
| 合计 |
50 |
