从参加高一年级迎新数学竞赛的学生中,随机抽取了 名学生的成绩进行统计分析.
名学生的成绩进行统计分析.
(1)完成下列频率分布表,并画出频率分布直方图;
(2)从成绩是[50,60)和[90,100)的学生中选两人,求他们在同一分数段的概率.
| 分 组 |
频数 |
频率 |
 |
2 |
|
 |
10 |
|
 |
20 |
|
 |
15 |
|
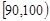 |
3 |
|
| 合 计 |
50 |
|

已知正项数列 中,
中, ,点
,点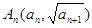 在抛物线
在抛物线 上.数列
上.数列 中,点
中,点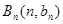 在经过点
在经过点 ,以
,以 为方向向量的直线
为方向向量的直线 上.
上.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)若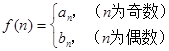 ,问是否存在
,问是否存在 ,使得
,使得 成立?若存在,求出
成立?若存在,求出 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(Ⅲ)对任意的正整数 ,不等式
,不等式 成立,求正数
成立,求正数 的取值范围.
的取值范围.
设椭圆

 的左、右焦点分别为
的左、右焦点分别为 ,
, ,上顶点为
,上顶点为 ,过
,过 与
与 垂直的直线交
垂直的直线交 轴负半轴于
轴负半轴于 点,且
点,且 .
.
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)若过 、
、 、
、 三点的圆恰好与直线
三点的圆恰好与直线 相切,求椭圆
相切,求椭圆 的方程;
的方程;
(Ⅲ)过 的直线
的直线 与(Ⅱ)中椭圆交于不同的两点
与(Ⅱ)中椭圆交于不同的两点 、
、 ,则
,则 的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
如图 ,在
,在 中,
中, °,
°, ,
,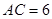 ,
, ,
, 分别是
分别是 ,
,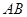 上的点,且
上的点,且 ,
, ,将
,将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图
,如图 .
.
(Ⅰ)求证: 平面
平面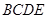 ;
;
(Ⅱ)若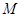 是
是 的中点,求
的中点,求 与平面
与平面 所成角的大小;
所成角的大小;
(Ⅲ)点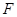 是线段
是线段 的靠近点
的靠近点 的三等分点,点
的三等分点,点 是线段
是线段 上的点,直线
上的点,直线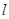 过点
过点 且垂直于平面
且垂直于平面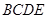 ,求点
,求点 到直线
到直线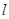 的距离的最小值.
的距离的最小值.
在数列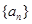 中,
中,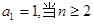 时,其前
时,其前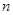 项和
项和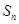 满足:
满足: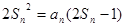 .
.
(Ⅰ)求证:数列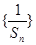 是等差数列,并用
是等差数列,并用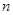 表示
表示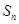 ;
;
(Ⅱ)令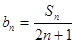 ,数列
,数列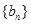 的前
的前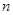 项和为
项和为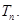 求使得
求使得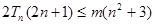 对所有
对所有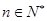 都成立的实数
都成立的实数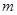 的取值范围.
的取值范围.
已知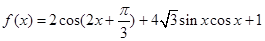 .
.
(Ⅰ)若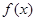 的定义域为
的定义域为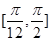 ,求
,求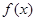 的值域;
的值域;
(Ⅱ)在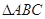 中,
中,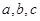 分别是
分别是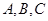 所对边, 当
所对边, 当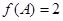 ,
,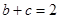 时,求
时,求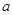 的最小值.
的最小值.