张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知, 该户型商品房的单价是8000元/ ,面积如图所示(单位:米,卫生间的宽未定,设宽为
,面积如图所示(单位:米,卫生间的宽未定,设宽为 米),售房部为张先生提供了以下两种优惠方案:
米),售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是8000元/ ,其中厨房可免费赠送
,其中厨房可免费赠送 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售

用
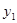 表示方案一中购买一套该户型商品房的总金额,用
表示方案一中购买一套该户型商品房的总金额,用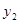 表示方案二中购买一套该户型商品房的总金额,分别求出
表示方案二中购买一套该户型商品房的总金额,分别求出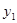 、
、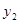 与
与 的关系式;
的关系式;
求
 取何值时,两种优惠方案的总金额一样多?
取何值时,两种优惠方案的总金额一样多?
张先生因现金不够,于2012年1月在建行借了9万元住房贷款,贷款期限为6年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月还款数额=平均每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率.
①张先生借款后第一个月应还款数额是多少元?
②假设贷款月利率不变,若张先生在借款后第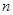 (
( ,
,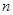 是正整数)个月的还款数额为P,请写出P与
是正整数)个月的还款数额为P,请写出P与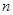 之间的关系式
之间的关系式
有理数a、b、c在数轴上的对应点如图所示:
化简代数式: .
.
先化简,再求值:
(1) ,其中:
,其中: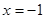 ,
, 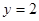 .
.
(2)已知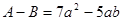 ,且
,且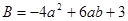 .
.
①求A等于多少;②若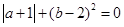 ,求A的值.
,求A的值.
(3)已知多项式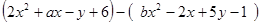 .
.
①若多项式的值与字母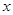 的取值无关,求
的取值无关,求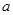 、
、 的值;
的值;
②在①的条件下,先化简多项式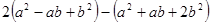 ,再求它的值.
,再求它的值.
化简:(1)
(2)
(共18分)计算:
(1)
(2)
(3)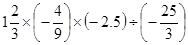
(4)
(5)
(6)
从2开始,连续的偶数相加,它们和的情况如下表:
(1)如果n=8时,那么S的值为________;
(2)由表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n=_________;
(3)由上题的规律计算300+302+304+…+2010+2012的值(要有计算过程).