如图.抛物线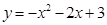 与x轴相交于点A和点B,与y轴交于点C.
与x轴相交于点A和点B,与y轴交于点C.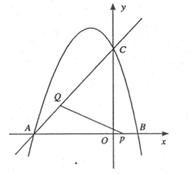
求点A、点B和点C的坐标
求直线AC的解析式
设点M是第二象限内抛物线上的一点,且
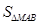 =6,求点M的坐标.
=6,求点M的坐标.
(满分6分)如图的数阵是由一些奇数组成的。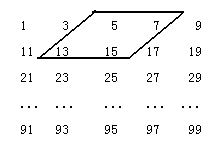
(1)形如图框中的四个数有什么关系?(可设第一行的第一个数为x,用含x的代数式表示另外三个数即可)。
(2)若这样框中的四个数的和是200,求出这四个数。
(3)是否存在这样的四个数,它们的和为2010..若存在,请求出这四个数中最大的数,若不存在请说明理由。
解方程(每小题4分,共8分)(1)、

(2)、

如图,Rt△ABC中,∠C=90°,BC=6,AC=8.点P,Q都是斜边AB上的动点,点P从B向A运动(不与点B重合),点Q从A向B运动,BP=AQ.点D,E分别是点A,B以Q,P为对称中心的对称点,HQ⊥AB于Q,交AC于点H.当点E到达顶点A时,P、Q同时停止运动.设BP的长为x,△HDE的面积为y.
(1)求证:△DHQ∽△ABC;
(2)求y关于x的函数解析式并求y的最大值;
(3)当x为何
 值时,△HDE为等腰三角形?
值时,△HDE为等腰三角形?
如图,已知矩形ABCD中,BC=6,AB=8,延长AD到点E,使AE=15,连结BE交AC于点P.
(1)求AP的长;
(2)若以点A为圆心,AP为半径作⊙A,试判断线段BE与⊙A的位置关系并说明理由;
(3)已知以点A为圆心,r1为半径的动OA,使点D在动⊙A的内部,点B在动⊙A的外部.
①则动⊙A的半径r1的取值范围是▲;
②若以点C为圆心,r2为半径的动⊙C与动⊙A相切,则r2的取值范围是▲.
已知P(-3,m)和Q(1,m)是抛物线y=2x2+bx+1上的两点.(1)求b的值;
(2)判断关于x的一元二次方程2x2+bx+1=0是否有实数根,若有,求出它的实数根;若没有,请说明理由;
(3)将抛物线y=2x2+bx+1的图象向上平移k(k是正整数)个单位,使平移后的图象与x轴无交点,求k的最小值.