如图，在直角梯形ABCD中，∠D =∠BCD = 90°，∠B = 60°，AB = 6，AD = 9，点E是CD上的一个动点（E不与D重合），过点E作EF∥AC，交AD于点F（当E运动到C时，EF与AC重合），把△DEF沿着EF对折，点D的对应点是点G,如图①．
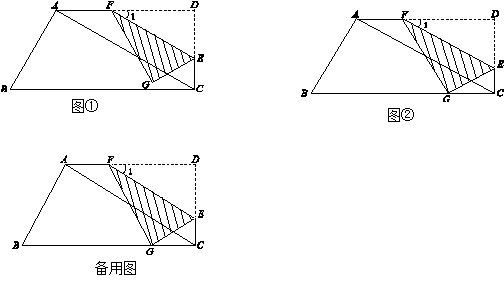
求CD的长及∠1的度数；
设DE = x，△GEF与梯形ABCD重叠部分的面积为y．
求y与x之间的函数关系式，并求x为何值时，y的值最大？最大值是多少？
当点G刚好落在线段BC上时,如图②,若此时将所得到的△EFG沿直线CB向左平移，速度为每秒1个单位，当E点移动到线段AB上时运动停止.设平移时间为t（秒）,在平移过程中是否存在某一时刻t，使得△ABE为等腰三角形？若存在，求出t的值；若不存在，请说明理由
已知：线段a，∠α．
求作：△ABC，使AB=BC=a，∠B=∠α．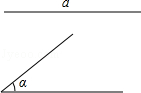
超市9月1日到5日的收入、支出情况如下表
| 日期 |
1日 |
2日 |
3日 |
4日 |
5日 |
| 支出（元） |
150 |
260 |
180 |
130 |
210 |
| 收入（元） |
160 |
240 |
150 |
180 |
300 |
运用你学的知识，给商店简单的记一笔帐．
（1）哪几天是亏本，那几天是盈利的？
（2）9月1日到5日，该超市总支出是多少？
张老师把七年级（一）班五名同学的成绩简记为：+15，-3，0，+6，-8，又知道记为0的成绩表示80分，正数表示超过80分，
（1）成绩最高的是多少分，成绩最低的是多少分？
（2）五名同学的平均成绩为多少分？
观察下列有规律的数：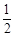
，
，
，
，
，
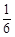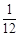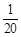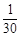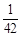……根据规律可知，
（1）第7个数_____________,第n个数是______________（n是正整数）．
（2） 
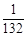是第__________个数．
（3）计算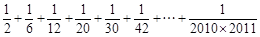
．（本题6分）
将连续的奇数1，3，5，7…排列成如下的数表用十字框框出5个数（如图），
（1）若将十字框上下左右平移，但一定要框住数列中的5个数，若设中间的数为a，用a的代数式表示十字框框住的5个数字之和；
（2）十字框框住的5个数之和能等于2020吗？若能，分别写出十字框框住的5个数；若不能，请说明理由；
（3）十字框框住的5个数之和能等于365吗？若能，分别写出十字框框住的5个数；若不能，请说明理由．（本题6分）