如图1,等腰25. 和等腰
和等腰 中,
中, ,
,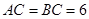 ,
,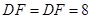 ,点
,点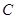 、
、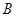 、
、 、
、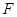 在一条直线上。当点
在一条直线上。当点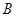 和点
和点 重合时,等腰
重合时,等腰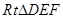 静止不动,等腰
静止不动,等腰 从
从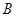 出发,沿线段
出发,沿线段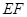 方向以每秒1个单位长度的速度匀速运动,当
方向以每秒1个单位长度的速度匀速运动,当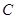 点与
点与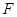 点重合时,停止运动。设运动时间为
点重合时,停止运动。设运动时间为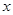 秒
秒 。
。

请填空:当
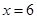 、12、14秒时,
、12、14秒时,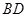 的长度分别为 、 、 ;
的长度分别为 、 、 ;在等腰
 的运动过程中,设等腰
的运动过程中,设等腰 和等腰
和等腰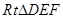 重叠部分的面积为
重叠部分的面积为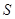 ,请直接写出
,请直接写出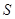 与
与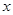 的函数关系式和相应的自变量
的函数关系式和相应的自变量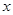 的取值范围;
的取值范围;如图2,当
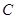 点与
点与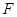 点重合时,将等腰
点重合时,将等腰 绕点
绕点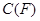 顺时针转
顺时针转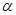 角(
角(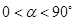 ),连接
),连接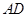 、
、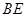 ,过点
,过点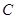 作
作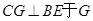 ,延长
,延长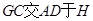 。
。
①求证: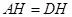 ;
;
②若 ,求
,求 的长度。
的长度。
如图,直线EF交直线AB、CD于点M、N,∠EMB=∠END,MG平分∠EMB,NH平分∠END。试问:图中哪两条直线互相平行?为什么?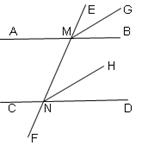
如图,已知,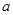 ∥
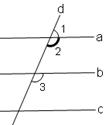
∥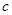 ,∠1+∠3=180º,请说明
,∠1+∠3=180º,请说明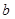 ∥
∥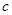 。
。
如图,已知AB∥CD∥EF,GC⊥CF,∠ABC=65º,∠EFC=40º,求∠BCG的度数。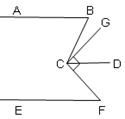
平面内的两条直线有相交和平行两种位置关系。
(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD +∠D,得∠BPD=∠B-∠D。将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;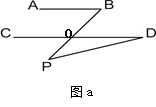
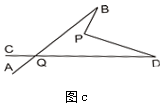
(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系? (不需证明);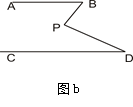
(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数。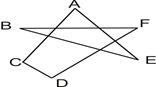

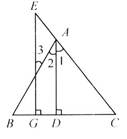
如图,已知AD⊥BC于D,EG⊥BC于G,∠E=∠3,AD平分∠BAC吗?若平分,请写出推理过程;若不平分,试说明理由.