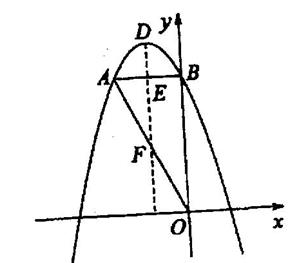
在平原上有一条笔直的公路,在公路同侧有A、B两个村庄。若以公路为 轴建立平面直角坐标系,如图1:已知A、B两个村庄的坐标分别为(2,2),(7,4),一辆汽车(看成点P)在
轴建立平面直角坐标系,如图1:已知A、B两个村庄的坐标分别为(2,2),(7,4),一辆汽车(看成点P)在 轴上行驶.
轴上行驶.汽车行驶过程中到A、B两村距离之和最小为多少?
汽车行驶过程中到A、B两村距离之差最大为多少?

如图,点B的坐标为(4,3),过点B作x轴的垂线垂足为A,交反比例函数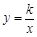 (x>0)图象于点C;连结OB交反比例函数
(x>0)图象于点C;连结OB交反比例函数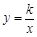 (x>0) 图象于点D,已知BC∶AB=2∶3。
(x>0) 图象于点D,已知BC∶AB=2∶3。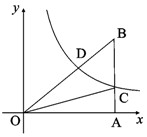
(1)求k的值
(2)求点D的坐标。
解方程: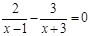 .
.
计算: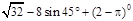
如图所示.P是⊙O外一点.PA是⊙O的切线.点A是切点.B是⊙O上一点.
且PA = PB,连接AO、BO、PO、AB,并延长BO与切线PA相交于点C.
(1)求证:PB是⊙O的切线 ;
(2)求证: AC · PC=" OC" · BC ;
(3)设∠AOC = ,若cos
,若cos =
= ,OC =" 15" ,求AB的长。
,OC =" 15" ,求AB的长。
如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连结OA.
(1)求B点的坐标;
(2)若抛物线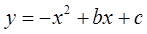 经过点A、B .
经过点A、B .
①求抛物线的解析式及顶点坐标;
②将抛物线竖直向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围.