如图，已知射线CB∥OA，∠C＝∠OAB＝140°，E、F在CB上，且满足OB平分∠AOF,OE平分∠COF
求∠EOB的度数。
若平行移动AB，那么∠OBC︰∠OFC的值是否随之发生变化？若变化，找出变化规律；若不变，求出这个值。
在平行移动AB的过程中，是否存在某种情况，使∠OEC＝∠OBA？若存在，请求出∠OEC和∠OBA的度数；若不存在，请说明理由。
如图（1），一群小孩以同样的速度同时从A村出发到B村，要过一条公路a,其中只有一个小孩用最快的时间到达B村。你知道这个聪明的小孩的行程路线吗？在图上标出示意图。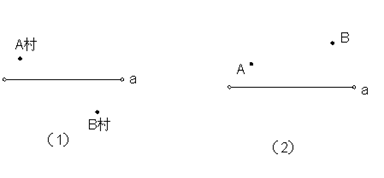
如图（2），在公路的同侧有两村庄，要在公路上建立一个站点，使到A、B两村的距离相等，请标出站点位置。
求下列各式的值：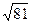
+（－6）－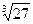
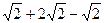
张慧同学给大家出了下面这样的问题，请你解答。
我的袋子里有3枚1角和1枚5角的硬币，如果我任意拿出两枚硬币，你知道前述之和大于5角的概率吗？
（要求：借助化树状图或列表的方法，列举所有等可能的结果，再进行计算。）
已知：关于x的方程
.求证：方程有两个不相等的实数根；
当
时，方程的两根之和为，两根之积为若方程的一个根是
，求
的值；
解方程：