如图所示,已知AB为⊙O的直径,CD是弦,且AB CD于点E.连接AC、OC、BC.
CD于点E.连接AC、OC、BC.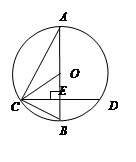
(1)求证: ACO=
ACO= BCD.
BCD.
(2)若EB=8cm,CD=24cm,求⊙O的直径.
探索证明如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD, BC,AC的中点.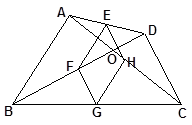
(1)求证:四边形EFGH是平行四边形;
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论.
(3)当AB和CD满足什么条件时,四边形EFGH是正方形.(直接写出结论,不必写证明过程)
应用题(10分 )某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售量可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢利市场,该店应按原售价的几折出售?
如图正方形ABCD边长为1,G为CD边上的一个动点(点G与C、D不重合),以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于点H.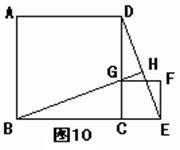
(1)求证:BH⊥DE
(2)当BH垂直平分DE时,求CG的长度?请说明理由.(提示:要有辅助线哟?)
解方程
(1)(x-1)2+2x(x-1)=0
(2) 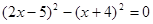
(3)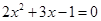 (用公式法)
(用公式法)
(4)(x-1)(x+2)=70
(本题10分)九(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.
小组讨论后,同学们做了以下三种试验: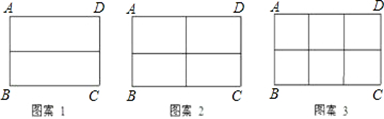
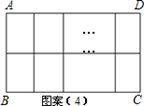
请根据以上图案回答下列问题:
(1)在图案1中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,长方形框架ABCD的面积是 m2;
(2)在图案2中,如果铝合金材料总长度为6m,设AB为xm,长方形框架ABCD的面积为S= (用含x的代数式表示);当AB= m时,长方形框架ABCD的面积S最大;在图案3中,如果铝合金材料总长度为am,设AB为xm,当AB= m时,长方形框架ABCD的面积S最大.
(3)经过这三种情形的试验,他们发现对于图案4这样的情形也存在着一定的规律.探索:如图案4如果铝合金材料总长度为am,共有n条竖档时,那么当竖档AB多少时,长方形框架ABCD的面积最大.(写出求解过程)