（本题10分）九（1）班数学兴趣小组在社会实践活动中，进行了如下的课题研究：用一定长度的铝合金材料，将它设计成外观为长方形的三种框架，使长方形框架面积最大．
小组讨论后，同学们做了以下三种试验：
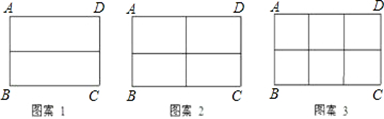
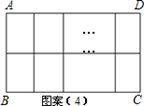
请根据以上图案回答下列问题：
（1）在图案1中，如果铝合金材料总长度（图中所有黑线的长度和）为6m，当AB为1m，长方形框架ABCD的面积是 m2；
（2）在图案2中，如果铝合金材料总长度为6m，设AB为xm，长方形框架ABCD的面积为S= （用含x的代数式表示）；当AB= m时，长方形框架ABCD的面积S最大；在图案3中，如果铝合金材料总长度为am，设AB为xm，当AB= m时，长方形框架ABCD的面积S最大．
（3）经过这三种情形的试验，他们发现对于图案4这样的情形也存在着一定的规律．探索：如图案4如果铝合金材料总长度为am，共有n条竖档时，那么当竖档AB多少时，长方形框架ABCD的面积最大．（写出求解过程）
若关于y的不等式
的整数解是-3、-2、-1、0、1，确定t的取值范围。
南昌地铁一号线即将开通,给南昌市民的出行带来变化．小王和小林准备利用课余时间，以问卷的方式对市民的出行方式进行调查．如图是南昌地铁一号线图（部分站名），小王和小林分别从A站、B站、C站这三站中,随机选取一站作为调查的站点．
⑴在这三站中,小王选取问卷调查的站点是A站的概率是多少？（请直接写出结果）
⑵请你用列表法或画树状图（树形图）法,求小王选取问卷调查的站点与小林选取问卷调查的站点相邻的概率．（各站点用相应的英文字母表示）
在∠MON的两边上分别找两点P、Q，使得AP+PQ+QB最小。（保留作图痕迹，不要求作法）
先化简，再求值：
， 其中
．
如图，在平面直角坐标系中，O为坐标原点，已知A（2，
），C（4,0），E点从O出发，以每秒1个单位的速度，沿边OC向C点运动，P点从O点出发，以每秒2个单位的速度，沿边OA与边AC向C运动，E、P两点同时出发，设运动时间为t秒。
（1）求∠AOC的度数，
（2）过 E作EH⊥AC于H，当t为何值时，△EPH是等边三角形。
（3）设四边形OEHP的面积S，求S关于t的函数表达式，并求出其最大值。
（4）当△OPE与以E、H、P为顶点的三角形相似，求P点坐标。