如图,在平面直角坐标系中,O为坐标原点,已知A(2, ),C(4,0),E点从O出发,以每秒1个单位的速度,沿边OC向C点运动,P点从O点出发,以每秒2个单位的速度,沿边OA与边AC向C运动,E、P两点同时出发,设运动时间为t秒。
),C(4,0),E点从O出发,以每秒1个单位的速度,沿边OC向C点运动,P点从O点出发,以每秒2个单位的速度,沿边OA与边AC向C运动,E、P两点同时出发,设运动时间为t秒。
(1) 求∠AOC的度数,
(2) 过 E作EH⊥AC于H,当t为何值时,△EPH是等边三角形。
(3)设四边形OEHP的面积S,求S关于t的函数表达式,并求出其最大值。
(4)当△OPE与以E、H、P为顶点的三角形相似,求P点坐标。
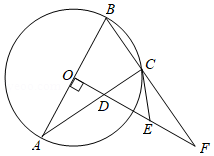
如图, 内接于 , 为直径,作 交 于点 ,延长 , 交于点 ,过点 作 的切线 ,交 于点 .
(1)求证: ;
(2)如果 , ,求弦 的长.
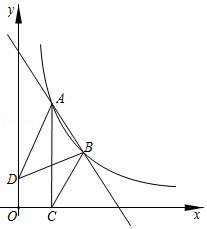
如图,点 , , 是直线 与反比例函数 图象的两个交点, 轴,垂足为点 ,已知 ,连接 , , .
(1)求直线 的表达式;
(2) 和 的面积分别为 , .求 .
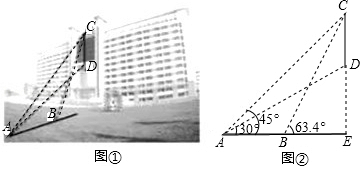
某数学兴趣小组要测量实验大楼部分楼体的高度(如图①所示, 部分),在起点 处测得大楼部分楼体 的顶端 点的仰角为 ,底端 点的仰角为 ,在同一剖面沿水平地面向前走20米到达 处,测得顶端 的仰角为 (如图②所示),求大楼部分楼体 的高度约为多少米?(精确到1米)
(参考数据: , , , ,
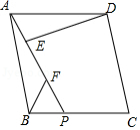
在菱形 中,点 是 边上一点,连接 ,点 , 是 上的两点,连接 , ,使得 , .
求证:(1) ;
(2) .
某商场的运动服装专柜,对 , 两种品牌的运动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表:
|
第一次 |
第二次 |
|
|
品牌运动服装数 件 |
20 |
30 |
|
品牌运动服装数 件 |
30 |
40 |
|
累计采购款 元 |
10200 |
14400 |
(1)问 , 两种品牌运动服的进货单价各是多少元?
(2)由于 品牌运动服的销量明显好于 品牌,商家决定采购 品牌的件数比 品牌件数的 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件 品牌运动服?