手工课时,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60 cm,菱形的面积S(单位:cm2)随其中一条对角线的长x(单位:cm)的变化而变化.请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
当x是多少时,菱形风筝面积S最大?最大面积是多少?______.
(参考公式:当x=-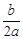 时,二次函数y=ax2+bx+c(a≠0)有最小(大)值
时,二次函数y=ax2+bx+c(a≠0)有最小(大)值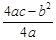 )
)
已知关于x的一元二次方程x +4x+m=O.
+4x+m=O.
(1)当m=l时,请用配方法求方程的根:
(2)若方程没有实数根,求m的取值范围.
⑴计算: 
⑵先化简,再求值: ,其中
,其中 。
。
如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣ ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的解析式及A、B两点的坐标;
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值,若不存在,请说明理由;
(3)以AB为直径的⊙M相切于点E,CE交x轴于点D,求直线CE的解析式.
某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.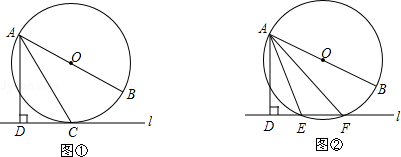
(1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线l与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.