某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
如图,Rt△OAB中,∠OAB=90°,O为坐标原点,边OA在x轴上,OA=AB=1个单位长度.把Rt△OAB沿x轴正方向平移1个单位长度后得△AA1B.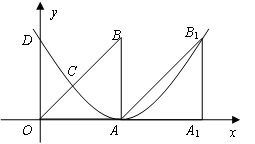
(1)求以A为顶点,且经过点B1的抛物线的解析式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.
透明的口袋里装有3个球,这3个球分别标有数字1、2、3,这些球除了数字外都相同。
(1)如果从袋中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?
(2)小明和小东玩摸球游戏,游戏规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小东随机摸出一个球,记下球的数字.谁摸出的球的数字大,谁获胜.现请你利用树状图或列表的方法分析游戏规则对双方是否公平?并说明理由。
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD= ,求⊙O的直径长.
,求⊙O的直径长.
某校八年级(3)班的师生到距离10千米的山区植树,出发1.5小时后,张锦同学骑自行车从学校按原路追赶队伍,结果他们同时到达植树地点.如果张锦同学骑车的速度比队伍步行的速度的2倍还多2千米.求骑车与步行的速度各是多少?
如图,在平面直角坐标系xoy中,一次函数 的图象与反比例函数
的图象与反比例函数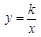 的图象的一个交点为A(-1,n).x轴上有点B,且△AOB的面积为3.
的图象的一个交点为A(-1,n).x轴上有点B,且△AOB的面积为3.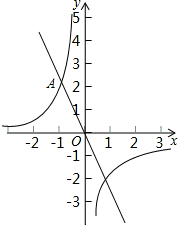
(1)求反比例函数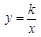 的解析式;
的解析式;
(2)求点B的坐标。