如图,梯形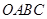 中,
中,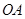 在
在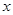 轴上,
轴上, ∥
∥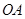 ,∠
,∠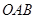 =
=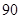 °,
°,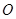 为坐标原点,
为坐标原点, ,
, ,动点
,动点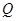 从点
从点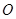 出发,以每秒1个单位的速度沿线段
出发,以每秒1个单位的速度沿线段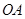 运动,到点
运动,到点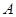 停止,过点
停止,过点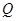 作
作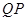 ⊥
⊥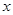 轴交
轴交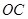 或
或 于点
于点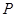 ,以
,以 为一边向右作正方形
为一边向右作正方形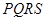 ,设运动时间为
,设运动时间为 (秒),正方形
(秒),正方形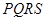 与梯形
与梯形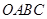 重叠面积为
重叠面积为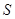 (平方单位).
(平方单位).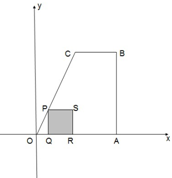
(1)求tan∠AOC.
(2)求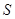 与t的函数关系式.
与t的函数关系式.
(3)求(2)中的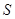 的最大值.
的最大值.
(4)连接 ,
, 的中点为
的中点为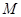 ,请直接写出在正方形
,请直接写出在正方形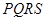 变化过程中,t为何值时,△
变化过程中,t为何值时,△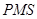 为等腰三角形.
为等腰三角形.
如图,已知OB的方向是南偏东60°,OA、OC分别平分∠NOB和∠NOE,
(1)请直接写出OA的方向是__________,OC的方向是__________.
(2)求∠AOC的度数.
学校组织同学到抗美援朝纪念馆参观,小丹因事没有和同学同时出发,于是准备在学校门口搭乘出租车赶去与同学们会合,出租车的收费标准是:起步价为5元,3千米后每千米收1.2元,不足1千米的按1千米计算。请你回答下列问题:
(1)小丹乘车3.8千米,应付费_________元.
(2)小丹乘车x(x是大于3的整数)千米,应付费多少钱?
(3)小丹身上仅有10元钱,乘出租车到距学校7千米远的抗美援朝纪念馆的车费够不够?请说明理由.
探索规律:将连续的偶数2,4,6,8, ,排成下表,如图: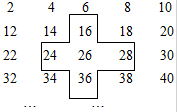
(1)十字框中的五个数的和与中间的数18有什么关系?
(2)设中间的数为x ,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五位数,其它五位数的和能等于2050吗?如能,写出这五位数,如不能,说明理由.
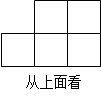
如图,是由一些大小相同的小正方体组成的简单几何体从正面和上面观察到的图形.
(1)若组成这个几何体的小正方体的块数为n,请你写出n的所有可能值;
(2)请你画出当n取最小值时这个几何体从左面观察到的图形.
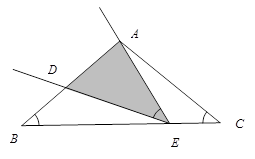
如图,在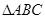 中
中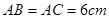 ,
,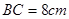 .点
.点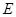 是线段
是线段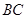 边上的一动点(不含
边上的一动点(不含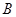 、
、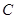 两端点),连结
两端点),连结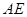 ,作
,作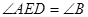 ,交线段
,交线段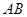 于点
于点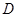 .
. 
(1)求证: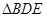 ∽
∽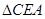 ;
;
(2)设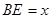 ,
,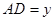 ,请写
,请写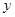 与
与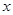 之间的函数关系式,并求
之间的函数关系式,并求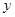 的最小值。
的最小值。
(3)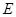 点在运动的过程中,
点在运动的过程中,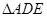 能否构成等腰三角形?若能,求出
能否构成等腰三角形?若能,求出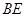 的长;若不能,请说明理由。
的长;若不能,请说明理由。