如图,直线y=﹣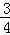 x+6分别与x轴、y轴交于A、B两点;直线y=
x+6分别与x轴、y轴交于A、B两点;直线y=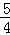 x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).
x与AB交于点C,与过点A且平行于y轴的直线交于点D.点E从点A出发,以每秒1个单位的速度沿x轴向左运动.过点E作x轴的垂线,分别交直线AB、OD于P、Q两点,以PQ为边向右作正方形PQMN.设正方形PQMN与△ACD重叠部分(阴影部分)的面积为S(平方单位),点E的运动时间为t(秒).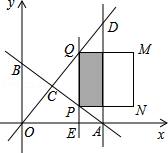
(1)求点C的坐标.
(2)当0<t<5时,求S与t之间的函数关系式,并求S的最大值。
(3)当t>0时,直接写出点(5,3)在正方形PQMN内部时t的取值范围。
已知一元二次方程k +(2k-1)x+k+2=0有两个不相等的实数根,求k的取值范围.
+(2k-1)x+k+2=0有两个不相等的实数根,求k的取值范围.
解方程: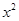 +3x-4=0
+3x-4=0
某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为
已知,矩形 中,
中,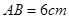 ,
,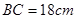 ,
, 的垂直平分线
的垂直平分线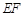 分别交
分别交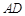 、
、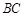 于点
于点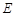 、
、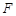 ,垂足为
,垂足为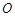 .
.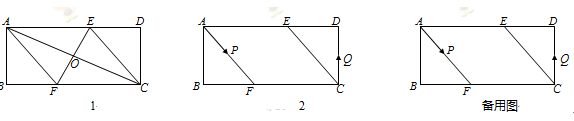
(1)如图26-1,连接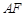 、
、 .求证四边形
.求证四边形 为菱形,并求
为菱形,并求 的长;
的长;
(2)如图26-2,动点 、
、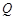 分别从
分别从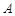 、
、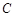 两点同时出发,沿
两点同时出发,沿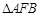 和
和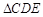 各边匀速运动一周.即点
各边匀速运动一周.即点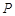 自
自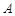 →
→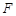 →
→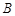 →
→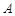 停止,点
停止,点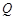 自
自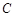 →
→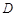 →
→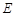 →
→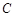 停止.在运动过程中.
停止.在运动过程中.
①已知点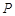 的速度为每秒10
的速度为每秒10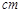 ,点
,点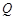 的速度为每秒6
的速度为每秒6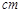 ,运动时间为
,运动时间为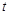 秒,当
秒,当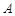 、
、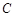 、
、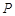 、
、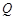 四点为顶点的四边形是平行四边形时,求
四点为顶点的四边形是平行四边形时,求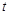 的值.
的值.
②若点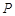 、
、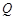 的运动路程分别为
的运动路程分别为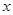 、
、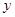 (单位:
(单位: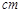 ,
, ),已知
),已知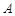 、
、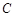 、
、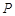 、
、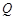 四点为顶点的四边形是平行四边形,求
四点为顶点的四边形是平行四边形,求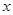 与
与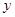 满足的函数关系式.
满足的函数关系式.
在平面直角坐标系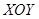 中,一次函数
中,一次函数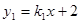 的图象与y轴交于点A,与x轴交于点B,与反比例函数
的图象与y轴交于点A,与x轴交于点B,与反比例函数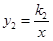 的图象分别交于点M、N,已知△AOB的面积为3,点M的纵坐标为4.
的图象分别交于点M、N,已知△AOB的面积为3,点M的纵坐标为4.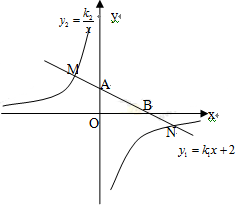
(1)求一次函数与反比例函数的解析式;
(2)求点N的坐标并直接写出当y1>y2时,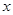 的取值范围.
的取值范围.