如图,在平面直角坐标系中,四边形 的顶点O为坐标原点,点C在x轴的正半轴上,且
的顶点O为坐标原点,点C在x轴的正半轴上,且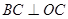 于点
于点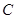 ,点
,点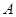 的坐标为(2,2
的坐标为(2,2 ),
), =
=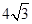 ,
,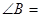 60°,点
60°,点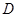 是线段
是线段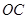 上一点,且
上一点,且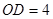 ,连接
,连接 .
.
(1)求证:△AOD是等边三角形;
(2)求点 的坐标;
的坐标;
(3)平行于 的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形
的直线l从原点O出发,沿x轴正方向平移.设直线l被四边形 截得的线段长为
截得的线段长为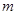 ,直线l与x轴交点的横坐标为t.
,直线l与x轴交点的横坐标为t.
① 当直线l与x轴的交点在线段CD上(交点不与点C,D重合)时,请直接写出m与t的函数关系式(不必写出自变量t的取值范围).
② 若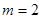 ,请直接写出此时
,请直接写出此时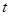 的值.
的值.
(满分6分)两种移动电话计费方式如下:
(1)一个月内某用户在本地通话时间是x分钟,请你用含有x的式子分别写出两种计费方式下该用户应该支付的费用。
(2)若某用户一个月内本地通话时间是5个小时,你认为采用哪种方式较为合算?
(3)小王想了解一下一个月内本地通话时间为多少时,两种计费方式的收费一样多。请你帮助他解决一下。
(满分5分)一个四边形的周长是48cm,已知第一条边长是acm,第二条比第一条边的2倍长3cm,第三条边等于第一、第二两条边的和。(1)用含a的代数式表示第四条边。
(2)当a=7时,还能得到四边形吗?说说理由。
(满分5分)作图并计算:把线段AB延长线到D,使BD= ,再延长线段BA到C,使CA=AD。
,再延长线段BA到C,使CA=AD。
求:(1)CD是AB的几倍?
(2)BC是CD的几分之几?
(满分6分)如图的数阵是由一些奇数组成的。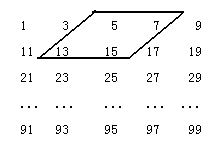
(1)形如图框中的四个数有什么关系?(可设第一行的第一个数为x,用含x的代数式表示另外三个数即可)。
(2)若这样框中的四个数的和是200,求出这四个数。
(3)是否存在这样的四个数,它们的和为2010..若存在,请求出这四个数中最大的数,若不存在请说明理由。
解方程(每小题4分,共8分)(1)、

(2)、
