某通讯器材公司销售一种市场需求较大的新型通讯产品．已知每件产品的进价为40元，每年销售该种产品的总开支（不含进价）总计120万元．在销售过程中发现，年销售量y（万件）随销售单价x（元）增大而减小，且年销售量y（万件）与销售单价x（元）之间存在着一次函数关系y=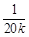
x+b，其中整数k使式子
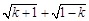有意义．经测算，销售单价为60元时，年销售量为50000件．求y与x的函数关系式；
试写出该公司销售该产品的年获利z（万元）关于销售单价x（元）的函数关系式（年获利=年销售额―年销售产品总进价―年总开支）．当销售单价x为何值时，年获利最大？并求这个最大值；
若公司希望该种产品一年的销售获利不低于40万元．请你帮助该公司确定销售单价的范围．在此情况下，要使产品销售量最大，你认为销售单价应定为多少元？
某旅行社的一则广告如下：“我社组团‘泰兴一日游’旅行，收费标准如下：如果人数不超过30人，人均旅游费用为80元；如果人数超过30人，那么每超出1人，人均旅游费用降低1元，但人
均旅游费用不得低于50元”．某单位组织一批员工参加了该旅行社的“泰兴一日游”，共付给旅行社旅游费用2800元，问该单位参加本次旅游的员工共多少人？
如图，A、B是泰兴公园游玩湖的两个景点，C为湖心一个景点．景点C在景点B的正西方向，从景点A看，景点C在北偏东30°方向，景点B在北偏东75°方向．一游客自景点A驾船以每分钟20米的速度行驶了8分钟到达景点C，之后又以同样的速度驶向景点B，该游客从景点C到景点B需用多长时间？（精确到1分钟）（参考数据：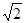
≈1.4
1、
≈1.73、sin75°≈0.97、cos75°≈0.26、tan75°≈3.73）
如图所示，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作BC的平行线交CE的延长线于点F，连接BF．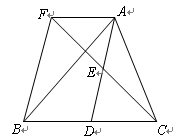
（1）求证：AF＝BD；
（2）如果AB＝AC，试证明：四边形AFBD为矩形．
甲、乙、丙3人站成一排合影留念．（1）甲站在中间的概率为▲；
（2）请用画树状图、列表或其他方法求甲、乙两人恰好相邻的概率
．
如图，△ABC中A(－2,－3),B(－3,－1),C(－1,－2)．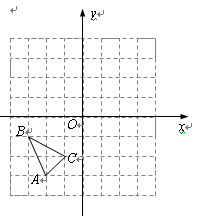
（1）画图：
①△ABC关于y轴对称的△A1B1C1；
②将△ABC向上平移4个单位长度后的△A2B2C2；
③将△ABC绕原点O旋转180°后的△A3B3C3．（2）填空：
①B1的坐标为▲，B2的坐标为▲，B3的坐标为▲；
②在△A1B1C1，△A2B2C2，△A3 B3C3中，
△▲与△▲成轴对称，对称轴是▲．